Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 24

A placa fina uniforme tem uma massa de 15   k g , imediatamente antes de seu canto A acertar o gancho, ela está caindo com uma velocidade v G = - 5 k   m / s sem movimento rotacional. Determine sua velocidade angular logo após o canto A acertar o gancho sem repicar.

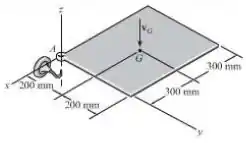
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Por definição, temos que:

I x = I x ' + m y G 2 + z G 2

I x = 1 12 15 0,4 2 + 15 0,2 2 + 0 2

I y = I y ' + m x G 2 + z G 2

I y = 1 12 15 0,6 2 + 15 - 0,3 2 + 0 2

I z = I z ' + m y G 2 + x G 2

I z = 1 12 15 0,4 2 + 0,6 2 + 15 - 0,3 2 + 0 , 2 2

Temos também que:

I x y = I x ' y ' + m x G y G

I x y = 0 + 15 ( - 0,3 ) ( 0,2 )

I x y = - 0.9   k g ⋅ m 2

I y z = I z ' y ' + m z G y G

I y z = 0 + 15 ( 0,2 ) ( 0 )

I y z = 0

I x z = I x ' z ' + m x G z G

I x z = 0 + 15 ( - 0,3 ) ( 0 )

I x z = 0

Passo 2

Podemos aplicar a conservação da quantidade de movimento angular:

H A 1 = - 0,3 i + 0,2 j × 15 ( - 5 k )

H A 1 = - 15 i - 22,5 j

Para o segudo momento, vamos analisar as componentes:

Em x :

H A 2 x = I x ω x - I x y ω y - I x z ω z

H A 2 x = 0,8 ω x - ( - 0,9 ) ω y - 0 ω z

H A 2 x = 0,8 ω x + 0,9 ω y

Em y :

H A 2 y = - I x y ω x + I y ω y - I y z ω z

H A 2 y = - - 0,9 ω x + 1,8 ω y - 0 ω z

H A 2 y = 0,9 ω x + 1,8 ω y

Em z :

H A 2 z = - I x z ω x - I y z ω y + I z ω z

H A 2 z = - 0 ω x - 0 ω y + 2,6 ω z

H A 2 z = 2,6 ω z

Agora que sabemos as componentes, temos:

H A 2 = 0,8 ω x + 0,9 ω y i + 0,9 ω x + 1,8 ω y j + 2,6 ω z k

H A 1 = H A 2

- 15 i - 22,5 j = 0,8 ω x + 0,9 ω y i + 0,9 ω x + 1,8 ω y j + 2,6 ω z k

- 15 = 0,8 ω x + 0,9 ω y

- 22,5 = 0,9 ω x + 1,8 ω y

0 = 2,6 ω z

Resolvendo, temos:

ω x = - 10,71   r a d / s

ω y = - 7,143   r a d / s

ω z = 0

Logo:

ω = - 10,71 i - 7,143 j

Resposta

ω = - 10,71 i - 7,143 j

Ver Outros Exercícios desse livro