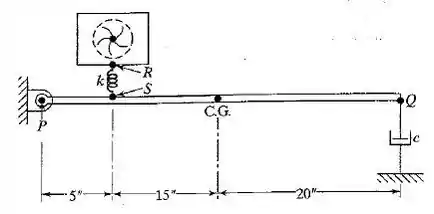
Uma placa rígida com de peso é articulada ao longo de uma borda e apoiada sobre um amortecedor de mola com in na borda oposta , como mostra a Figura . Um pequeno exaustor com de peso, que gira a 750 rpmé montado sobre a placa por meio de uma mola com / in. Se o centro de gravidade do exaustor estiver localizado a 0,1 in de seu eixo de rotação, determine o movimento em regime permanente da borda e a força transmitida ao ponto .
Passo 1
Peso da placa 500 N, Dashpot C = 200 N-s / m
Peso do ventilador 200 N, girando a 750 rpm, Mola k = 40kN / m
O centro de gravidade do ventilador é de 3 mm de deslocamento do eixo de rotação.
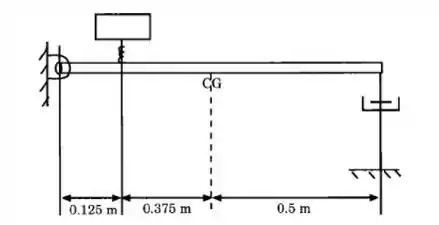
Passo 2
Solução
Passo 3
O ponto R está sujeito à força
Suponha que S não esteja se movendo. Então R é deslocado por
Passo 4
deslocamento angular da placa PQ. Deslocamento de S Extensão da mola Restaurando o momento da força da mola sobre P Velocidade de 1) Força de amortecimento em
Momento da força de amortecimento em Equação do movimento da placa PQ:
(E1)
Comparando E1 com Eq 3.24
Em que das Eqs 3.30 e 3.31, temos
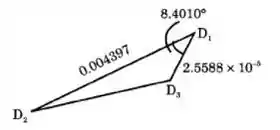
Passo 5
Estado estacionário do movimento de
Deslocamento de