Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 5.Problemas - Ex. 5

Uma ponte rolante elétrica, composta por uma trave, um carrinho e um cabo, é mostrada na Figura 5.20. A trave tem uma resistência à flexão ( E I ) de 6 × 10 12 l b ⋅ i n 2 e um vão ( L ) de 30 f t . O cabo é feito de aço e tem um comprimento ( t ) de 20 f t . Os pesos do carrinho e da carga içada são 8000 l b e 2000 l b , respectivamente. Determine a área da seçāo transversal do cabo de modo que a frequência natural fundamental seja maior do que 20   H z .

Passo 1

Rigidez da viga = 48 E I l 3 = 48 17 × 10 9 9 3 = 1.11934 × 10 9 N / m

Rigidez da corda = A E l = A 200 × 10 9 6 = 3.3333 × 10 10 A N / m

m 1 = m a s s a   do carrinho = 3600 kg

m 2 =   m a s s a   d e   c a r g a   = 900 k g

Valor da frequência desejada: ω 1 > 20 H z .   L e t   ω 1 ≈ 25 H z = 157.08 r a d / s e c ou ω 1 2 ≈ 24674.1264 ( r a d / s e c ) 2

Frequência natural fundamental é dada por (veja Eq.(E3) na solução do problema 5.1)

ω 1 2 = k g + k 2 m 1 + k 2 m 2 - 1 4 k g + k m 1 + k m 2 2 - k g k m 1 m 2 (1)

Passo 2

Usando os valores conhecidos de kg, m1 e m2, uma série de valores de teste de A são dados e a Eq. (1) é avaliado para encontrar os valores correspondentes de   ω 1 2 . Os resultados são apresentados na tabela abaixo.

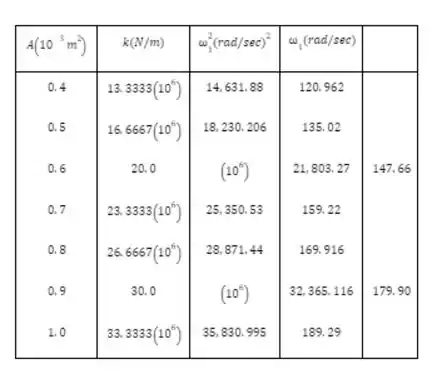
Pode ser visto que A = 0.7 × 10 - 3 m 2 produzirá uma frequência que melhor satisfaça ω = 157.08 r a d / s e c

Resposta

Pode ser visto que A = 0.7 × 10 - 3 m 2 produzirá uma frequência que melhor satisfaça ω = 157.08 r a d / s e c

Ver Outros Exercícios desse livro