Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 173

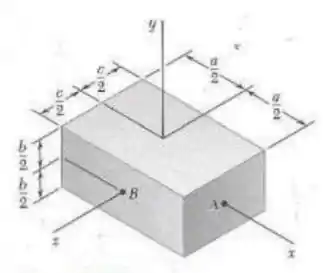
Para o prisma retangular mostrado na figura, determine os valores das razões b / a e c / a para que o elipsoide de inércia do prisma seja uma esfera quando calculado a no ponto A , b no ponto B .

Passo 1

Para nos auxiliar nesse problema vamos utilizar uma imagem dada no livro que é a seguinte

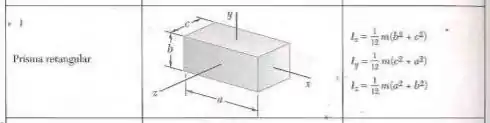
Além dessa imagem vamos utilizar o teorema dos eixos paralelos para calcularmos o que o problema deseja para o ponto A e para o ponto B .

Passo 2

Da imagem temos que

I x ' = 1 12 ⋅ m ⋅ b 2 + c 2  

  I y ' = 1 12 ⋅ m ⋅ a 2 + c 2 + m ⋅ a 2 2 = 1 12 ⋅ m ⋅ 4 a 2 + c 2

I z ' = 1 12 ⋅ m ⋅ a 2 + b 2 + m ⋅ a 2 2 = 1 12 ⋅ m ⋅ 4 a 2 + b 2

Observando a simetria do problema isso implica em: I x ' y ' = I y ' z ' = I z ' x ' = 0 . Agora, podemos utilizar a equação presente no livro dada por

I x ' ⋅ x 2 + I y ' ⋅ y 2 + I z ' ⋅ z 2 = 1

→   1 12 ⋅ m ⋅ b 2 + c 2 ⋅ x 2 + 1 12 ⋅ m ⋅ 4 a 2 + c 2 ⋅ y 2 + 1 12 ⋅ m ⋅ 4 a 2 + b 2 ⋅ z 2 = 1

Para que o elipsoide de inércia seja uma esfera devemos ter os coeficientes iguais. Portanto

1 12 ⋅ m ⋅ b 2 + c 2 = 1 12 ⋅ m ⋅ 4 a 2 + c 2 = 1 12 ⋅ m ⋅ 4 a 2 + b 2

→ b 2 + c 2 = 4 a 2 + c 2 → b a = 2  

De maneira análoga teremos

c a = 2  

Passo 3

Utilizando raciocínio semelhante, mas agora para o ponto B   vamos ter

I x ' = 1 12 ⋅ m ⋅ b 2 + c 2   m ⋅ c 2 2 = 1 12 ⋅ m ⋅ 4 c 2 + b 2

  I y ' = 1 12 ⋅ m ⋅ a 2 + c 2 + m ⋅ c 2 2 = 1 12 ⋅ m ⋅ a 2 + 4 c 2

I z ' = 1 12 ⋅ m ⋅ a 2 + b 2

Observando a simetria do problema isso implica em: I x ' y ' = I y ' z ' = I z ' x ' = 0 . Por fim, de maneira igual ao que foi feito para o ponto A vamos ter

1 12 ⋅ m ⋅ 4 c 2 + b 2 = 1 12 ⋅ m ⋅ a 2 + 4 c 2 = 1 12 ⋅ m ⋅ a 2 + b 2

O que implica em

b 2 + 4 c 2 = a 2 + 4 c 2 → b a = 1  

b 2 + 4 c 2 = a 2 + b 2 → c a = 1 2

Resposta

a b a = c a = 2

b b a = 1   e c a = 1 2

Ver Outros Exercícios desse livro