Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 113

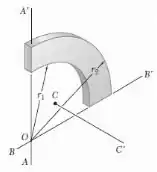
Um quato de anel mostrado na figura tem massa m e foi cortado de uma placa delgada uniforme. Sabendo que r 1 = 3 4 r 2 determine o momento de inércia de massa de um quarto de anel em relação a ao eixo A A ' , b ao eixo centroidal C C ' perdendicular ao plano de um quarto de anel.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O momento de inércia da placa delgada de um quarto de anel é equivalente à sua massa:

I m a s s a = ρ t I á r e a

I m a s s a = m A I á r e a

I m a s s a = m π 4 r 2 2 - r 1 2 I á r e a

Passo 2

O momento de inércia de massa de A A ' é:

I A A ' ,   á r e a = π 16 r 2 4 + r 1 4

I A A ' ,   m a s s a = m π 4 r 2 2 - r 1 2 π 16 r 2 4 + r 1 4

Como r 1 = 3 4 r 2 , temos que:

I A A ' ,   m a s s a = 25 64 m r 2 2

Passo 3

O momento de inércia de massa do eixo C C ' é dado por:

I D D ' ,   m a s s a = I A A ' ,   m a s s a + I B B ' ,   m a s s a

Logo:

I D D ' ,   m a s s a = 25 64 m r 2 2 + 25 64 m r 2 2

I D D ' ,   m a s s a = 25 32 m r 2 2

Agora analisando a localidade do centroide, temos que:

x - π 4 r 2 2 - r 1 2 = 4 r 2 3 π π 4 r 2 2 - 4 r 1 3 π π 4 r 1 2

x - = 4 3 π r 2 3 - r 1 3 r 2 2 - r 1 2

Portanto o centroide r - será:

r - = x - 2

r - = 4 2 3 π r 2 3 - 3 4 r 2 3 r 2 2 - 3 4 r 2 2

r - = 37 2 21 π r 2

Passo 4

Finalmente, temos que:

I D D ' ,   m a s s a = I C C ' ,   m a s s a + m r - 2

I C C ' ,   m a s s a = 25 32 m r 2 2 - m 37 2 21 π r 2 2

I C C ' ,   m a s s a 0,1522 m r 2 2

Resposta

a ) I A A ' ,   m a s s a = 25 64 m r 2 2

b ) I C C ' ,   m a s s a 0,1522 m r 2 2

Ver Outros Exercícios desse livro