Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 119

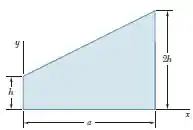
A superfície plana mostrada na figura é girada em torno do eixo x para formar um corpo de revolução homogêneo de massa m . Usando integração direta, expresse o momento de inércia do corpo em relação ao eixo x em termos de m e h .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Primeiramente, vamos definir a equação de r para este perfil:

r = y

r = 2 h - h a x + h

r = h a x + a

Passo 2

A nossa diferencial de massa d m deve ser expressa em função da densidade, sendo assim:

d m = ρ π r 2 d x

m = ∫ 0 a ρ π h a x + a 2 d x

Resolvendo, temos que:

m = 7 3 ρ π a h 2

Passo 3

Agora, para esse componente, vamos calcular o momento e a inércia pela integral:

I = ∫ 0 m 1 2 r 2 d m

I = ∫ 0 a 1 2 r 2 ρ π r 2 d x

I = ∫ 0 a 1 2 r 4 ρ π d x

I = ∫ 0 a 1 2 h a x + a 4 ρ π d x

Resolvendo, temos:

I = 31 10 ρ π a h 4

Passo 4

Substituindo ρ π a h 2 por 3 7 m , podemos dizer que:

I = 31 10 3 7 m h 2

I = 93 70 m h 2

Resposta

I = 93 70 m h 2

Ver Outros Exercícios desse livro