Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 21.Problemas - Ex. 76
O raio de giração em relação a um eixo passando pelo eixo de simetria do satélite de 2,5 Mg é , e em relação a qualquer eixo transversal passando pelo centro de massa G, . Se o satélite tem uma precessão em regime estacionário (steady-state) de duas revoluções por hora em torno do eixo Z, determine a taxa de rotação em torno do eixo z.
Passo 1
Começaremos o exercício calculando os momentos de inércia com relação ao eixo z e aos eixos transversais passantes pelo centro de massa G:
Passo 2
Agora, com o auxílio do diagrama a seguir:
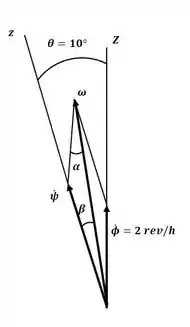
Podemos aplicar a mesma equação usada no problema 74 para descobrir o valor de :
Passo 3
Agora, com o auxílio do recorte do diagrama apresentado no passo 2:
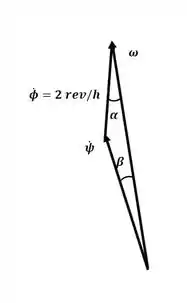
Sabemos que:
Com isso, podemos aplicar a lei dos senos para encontrar o valor de :