O redutor de velocidade está sujeito aos momentos de binário mostrados na figura. Determine o momento de binário resultante, especificando sua intensidade e os ângulos diretores coordenados.
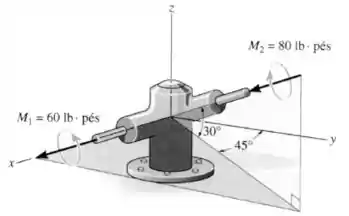
Passo 1
Vamos começar escrevendo cada um dos momentos em forma vetorial:
E para o vetor precisamos ter um pouco mais de cuidado, pois temos que projetá-lo em mais de uma etapa, a primeira para colocá-lo no plano , e depois de novoo para achar as componentes nesse plano:
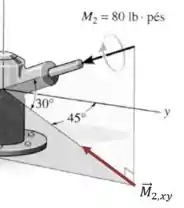
E a partir daí podemos calcular suas componentes em e :
E para a componente não precisamos de duas projeções, basta usar o ângulo de .
Agora podemos fazer a soma vetorial desses dois momentos para encontrar :
Passo 2
Agora vamos calcular a intensidade desse vetor:
E para encontrar o ângulo que o vetor forma com um eixo qualquer, só precisamos usar a seguinte fórmula:
Fazendo isso para cada um dos eixos, temos os seguintes resultados:
Onde , e são os ângulos formados pelo vetor com os eixos , e , respectivamente.
Resposta
O momento de binário resultante tem intensidade , e os ângulos diretores são , e (, e , respectivamente).