Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 45
Resolva o Problema 7.23 usando o círculo de Mohr.
Passo 1
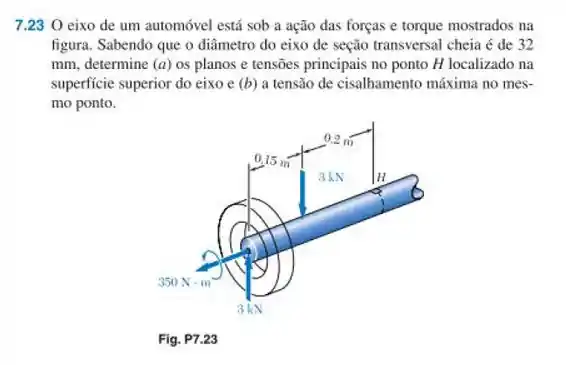
Tá legal! Para encontrar os planos e tensões principais no ponto H pedidos na letra (a), precisamos ter o círculo de Mohr desenhado para esse ponto. Só que para desenhar o círculo, precisamos das tensões aplicadas nesse ponto, que serão geradas pela torção e pelo momento aplicadas na barra. Então vamos precisar encontrar esses valores antes.
Com o círculo desenhado e os valores encontrados, vem a parte fácil, vamos aplicar as fórmulas para encontrar a tensão média e o raio do círculo, e aí conseguimos encontrar os planos e tensões principais para o ponto H.
E, para a letra (b), vamos usar também o círculo de Mohr para encontrar a tensão de cisalhamento máximo. Então vamos lá!
Passo 2
Vamos começar lembrando a equação para a tensão de cisalhamento gerada por torção, que é dada por:
Em que T é o torque aplicado, c é a distância do centro até o ponto de interesse e J é o momento polar de inércia, lembrando que o momento polar de inércia é dado por:
Substituindo essa expressão na equação para a tensão de cisalhamento e sabendo que nosso ponto H está na superfície, ou seja, em , a equação se torna:
Então, substituindo os valores conhecidos nessa equação, ambos dados no enunciado, teremos:
Passo 3
Agora nós vamos encontrar a tensão normal causado pelo momento fletor que existe na barra. Lembrando que essa tensão pode ser escrita como:
Em que M é o momento no ponto de interesse, y é a distância do centro até o ponto de estudo e I é o momento de inércia da barra. Beleza, sabemos que no nosso caso, a distância y vai ser o próprio raio da seção, ou seja:
Beleza, agora vamos calcular o momento no ponto H. Sabendo que o momento é a força vezes o braço de alavanca, para o nosso caso teremos:
Beleza! Agora falta o momento de inércia, que para uma seção circular é dado por:
Substituindo o valor do raio fornecido no enunciado, teremos:
Agora sim podemos encontrar o valor da tensão no ponto H, então teremos:
Passo 4
Beleza! Agora que encontramos as tensões, podemos desenhar o elemento diferencial de tensões para o ponto H, onde teremos:
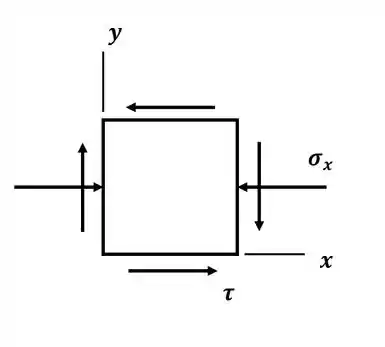
Então, as tensões para esse elemento diferencial serão:
Com isso, podemos calcular o valor da tensão média, que será dada por:
Então, teremos os seguintes pontos para o círculo de Mohr:
E, agora então podemos encontrar o raio para círculo de Mohr, que é dado pela fórmula:
Substituindo os valores conhecidos, teremos:
Passo 5
Com as informações que encontramos no passo 4, temos tudo o que precisamos para esboçar o círculo de Mohr, que então será:
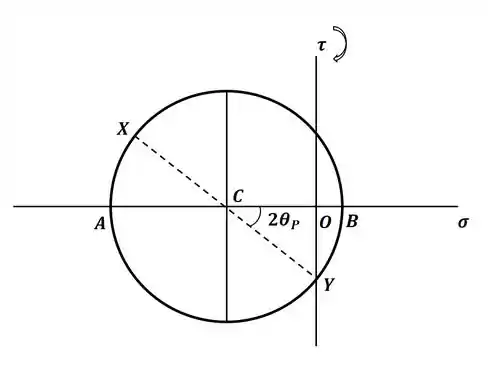
Então, para encontrar a inclinação do plano de tensão principal, por trigonometria, teremos:
Substituindo os valores conhecidos, teremos:
Esse é um dos planos, o outro obtido rotacionando o elemento diferencial em 90°, sendo assim, temos:
E, para finalizar a letra (a), basta encontrar as tensões principais nos pontos A e B do círculo, onde teremos:
Fechamos a letra (a), estamos quase lá! Bora pra (b)!
Passo 6
A (b) agora ficou fácil, a tensão de cisalhamento máxima nesse ponto será o próprio raio do círculo de Mohr do passo 5, já que o círculo é simétrico com relação ao eixo da tensão normal. Dessa forma, teremos: