Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 133

Resolver o prob. 3.132 assumindo que a placa de metal tenha sido dobrada na forma de um tubo de seção transversal quadrada de lado c.

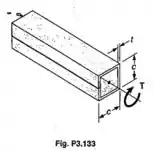
Passo 1

Basicamente estamos trabalhando com duas situações diferentes.

Na primeira situação, temos um Eixo Vazado de Paredes Finas, e nesse caso usamos as equações:

Na segunda situação, quando a união falha, temos uma barra não circular! E nesse caso as equações serão:

Passo 2

Começamos pela primeira situação!

Logo de cara dá para a gente calcular a área média interna a e dá para calcular o perímetro médio. Lembre-se que o perímetro médio é igual a integral de linha ∮ d s

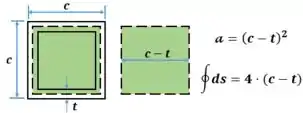
E com isso dá para a gente calcular a tensão

τ 1 = T 2 t a ⇒ τ 1 = T 2 ⋅ t ⋅ c - t 2

E o ângulo de torção:

ϕ 1 = T L 4 a 2 G ∮ d s t = T L 4 ⋅ c - t 4 ⋅ G ⋅ 4 c - t t ⇒ ϕ 1 = T L c - t 3 ⋅ t ⋅ G

Passo 3

Beleza!

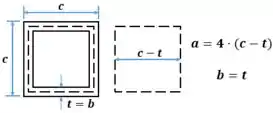
Agora vamos calcular a segunda situação. Como esta é uma situação de paredes finas, então podemos considerar a última linha da Tabela de Coeficientes para a torção em barras retangulares:

E agora vamos calcular a tensão

τ 2 = T c 1 a b 2 = T 0,333 ⋅ 4 ( c - t ) ⋅ t 2 ⇒ τ 2 ≈ 3 T 4 ( c - t ) t 2

E o ângulo de torção:

ϕ 2 = T L c 2 a b 3 G = T L 0,333 ⋅ 4 ( c - t ) ⋅ t 3 ⋅ G ⇒ ϕ 2 ≈ 3 T L 4 c - t t 3 G

Passo 4

Pronto, está praticamente tudo resolvido, agora só precisamos calcular as relações que a questão pede:

Primeiro τ 2 / τ 1 :

τ 2 τ 1 = 3 T 4 ( c - t ) t 2 T 2 ⋅ t ⋅ c - t 2 = 3 T 4 ( c - t ) t 2 ⋅ 2 ⋅ t ⋅ c - t 2 T ⇒ τ 2 τ 1 = 3 2 t c - t

E agora ϕ 2 / ϕ 1 :

ϕ 2 ϕ 1 = 3 T L 4 c - t t 3 G T L c - t 3 ⋅ t ⋅ G = 3 T L 4 c - t t 3 G ⋅ c - t 3 ⋅ t ⋅ G T L ⇒ ϕ 2 ϕ 1 = 3 c - t 2 4 t 2

Resposta

τ 2 τ 1 = 3 2 t c - t

ϕ 2 ϕ 1 = 3 c - t 2 4 t 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra de aço é usinada no feitio mostrado, constituindo um eixo com a forma de um tronco de cone, no qual troques de intensidade T = 8,5 kN.m são aplicados. Considerando que o aço é elastoplástico
Uma barra de aço é usinada no feitio mostrado, constituindo um eixo com a forma de um tronco de cone, no qual troques de intensidade T = 8,5 kN.m são aplicados. Considerando que o aço é elastoplástico
O eixo sólido mostrado é de um aço doce o qual se considera elastoplástico com G=77GPa e τ=145MPa. Determinar a intensidade do torque T, para que a zona plástica tenha 6,35 mm e 19 mm de profundidade.
Um eixo vazado mostrado é feito de um aço doce, o qual se considera ser elastoplástico com G = 77 GPa e τ=145MPa. Determinar a intensidade do torque T.
Uma barra de aço é usinada no feitio mostrado, constituindo um eixo com a forma de um tronco de cone, no qual troques de intensidade T = 8,5 kN.m são aplicados. Considerando que o aço é elastoplástico