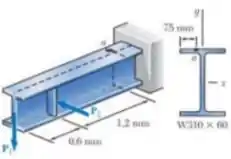
Passo 1
Na seção contendo os pontos a e b.
Para W310x60
Tensão normal no ponto a:
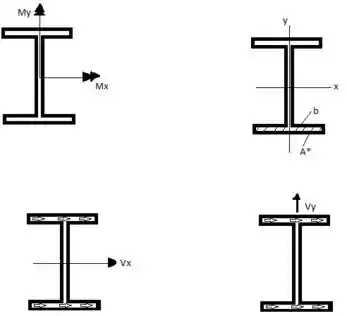
Passo 2
Tensão de cisalhamento no ponto b:
Considerando o esboço temos:
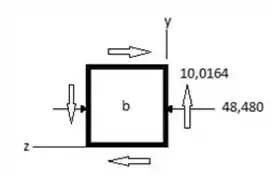

Na seção contendo os pontos a e b.
Para W310x60
Tensão normal no ponto a:

Tensão de cisalhamento no ponto b:
Considerando o esboço temos:
