Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 53

Três placas de aço, cada uma com 13mm de espessura, são soldadas para formar uma viga em balanço. Para o carregamento mostrada, determine as tensões normal e de cisalhamento nos pontos a e b

Passo 1

Sistema força par equivalente na seção contendo ponto H, considere o esboço abaixo ...

F x = 9 k N ,   F y = - 13 k N ,   F z = 0 k N

M x = 0,400 13 x 10 3 = 5200 N ∙ m     M y = 0,400 9 x 10 3 = 3600 N ∙ m

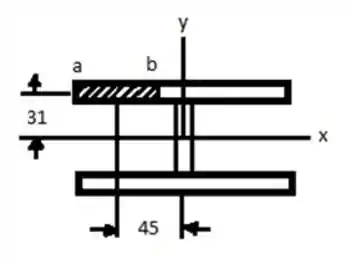
Agora temos que determinar a área e a inércia em X e Y ;) vem comigo :D

M z = 0

A = 2 150 13 + ( 13 ) ( 75 - 26 ) = 4537 m m 2

= 4537 x 10 - 6 m 2

I x = 2 1 12 150 13 3 + 150 13 37,5 - 6,5 2 + 1 12 13 75 - 26 3 = 3,9303 x 10 6 m m 4 = 3,9303 x 10 - 6 m 4

I y = 2 ∙ 1 12 13 150 3 + 1 12 75 - 26 13 3 = 7,3215 x 10 6 m m 4

= 7,3215 x 10 - 6 m m 4

Passo 2

Para o ponto a,

Q x = 0 ,   Q y = 0

Para o ponto b,

A * = ( 60 13 = 780 m m 2

x - = - 45 m m   y - = 31 m m

Q x = A * y - = 24,18 x 10 3 m m 3 = 24,18 x 10 - 6 m 3

Q y = A * x - = - 35,1 x 10 - 3 m m 3 = - 35,1 x 10 - 6 m 3

No ponto a,

σ = M x y I x - M y x I y = 5200 37,5 x 10 - 3 3,9303 x 10 - 6 - 3600 - 75 x 10 - 3 7,3215 x 10 - 6                       σ = 86,5 M P a

τ = 0

Passo 3

No ponto b,

σ = M x y I x - M y x I y = 5200 37,5 x 10 - 3 3,9303 x 10 - 6 - 3600 - 15 x 10 - 3 7,3215 x 10 - 6   = 57,0 M P a

Determinando a tensão de cisalhamento, temos :D

τ = V x Q y I y t + V y Q x I x t = 9 x 10 3 35,1 x 10 - 6 7,3215 x 10 - 6 13 x 10 - 3 + 13 x 10 3 24,18 x 10 - 6 3,9303 x 10 - 6 13 x 10 - 3 = 3,32 M P a + 6,15 M P a                  

  τ = 9,47 M P a

Resposta

  1.       σ = 86,5 M P a   e τ = 0
  2. τ = 9,47 M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo de madeira com diâmetro interno de 0,9 m é atado com aros de aço cuja área de seção transversal é 125 mm². Se a tensão admissível para os aros for σadm = 84 MPa, determine o espaçamento máximo
O tubo de extremidade aberta feito de cloreto de polivinil tem diâmetro interno de 100 mm e espessura de 5 mm. Se transportar água corrente à pressão de 0,42 MPa, determine o estado de tensão nas pare
Determine a força máxima P que pode ser exercida em cada um dos dois pistões de modo que a componente da tensão circunferencial no cilindro não ultrapasse 3 MPa. Cada pistão tem raio de 45 mm e a espe
Determine o valor da carga P que provocará a tensãonormal máxima σ m á x á = 200 MPa na seção a-a do elo.
Se P = 15 kN, desenhe o gráfico da distribuição de tensão que age na seção transversal a-a do elo fora de centro.