Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 81

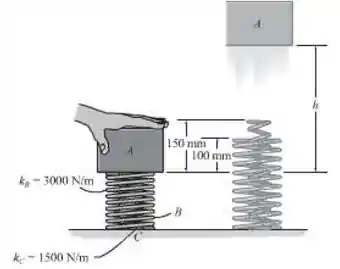
O bloco A de 15 kg é colocado sobre o topo de duas molas alinhadas, B e C, e, em seguida, é empurrado para baixo na posição mostrada. Se ele é solto em seguida, determine a sua altura máxima h que ele subirá.

Passo 1

Adotando um mecanismo onde o trabalho é realizado somente via forças conservativas, a hipótese conservação da energia mecânica é válida e descrita por:

E M e c = c o n s t a n t e

E M e c =   T + V = c o n s t a n t e

Passo 2

Adequando ao problema, pode-se supor que o estado 1 é o inicial e aquele representado pela subida do corpo A como o 2. Portanto, a conservação de energia pode ser reescrita em função das forças atuantes no sistema, a energia cinética oriunda da velocidade do corpo e energia potencial elástica através das molas:

T 1 + V 1 = T 2   +   V 2

Passo 3

Note que o sistema sofrerá influência da energia cinética e da energia potencial, sendo que a potencial irá contribuir de forma gravitacional e elástica através das molas. Assim, para o estado 01:

V 1 =   V g 1 +   V e 1

Tal que V e 1 é constituída pelo efeito das duas molas:

V e 1 =     k 1 s e 1 2 2 +   k 2 s i 1 2 2

V 1 = V g 1 +   k 1 s e 1 2 2 +   k 2 s i 1 2 2

V 1 = [ m g y 1 +   k 1 s e 1 2 2 +   k 2 s i 1 2 2 ]

Para o estado 02:

V 2 = m g y 2 +   k 1 s e 2 2 2 +   k 2 s i 2 2 2

O que é análogo para energia cinética, desse modo:

T 1 =     m v e 1 2 2 +   m v i 1 2 2

Para o estado 02:

T 2   =     m v e 2 2 2 +   m v i 2 2 2

Desse modo, aplicando à lei de conservação de energia:

T 1 + V 1 = T 2   +   V 2

  m v e1 2 2 +  m v i1 2 2 +mg y 1 +    k 1 s e1 2 2 +  k 2 s i1 2 2 =   m v e2 2 2 +  m v i2 2 2 +m g y 2 +  k 1 s e2 2 2 +  k 2 s i2 2 2

Passo 4

Determinada a equação que rege o fenômeno estudado, é necessário verificar as condições as quais cada estado está submetido. Desse modo:

  • Molas comprimidas em repouso ( v e =   v i = 0) no estado 01.
  • Molas sem deformação ( s e   = s i = 0) e em repouso ( v e =   v i = 0) no estado 02.

Adequando a expressão às condições analisadas:

0 + 0 +0+    3000 * 0,1 2 2 +  1500 * 0,15 2 2 = 0 + 0 +15*9,81*h+ (0 + 0)

  15   +  16,875   = 147,15*h

  31,875   = 147,15*h

h =   31,875 147,15             ∴           h = 0,21662   m

Resposta

A altura máxima alcançada é 0,21662 m.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando o módulo lunar foi deixado à deriva após o retorno de dois dos astronautas da Apollo ao módulo de comando, que orbitava a Lua a uma altitude de 140k m , sua velocidade foi reduzida para deixá--
Sabendo que a velocidade de uma sonda espacial experimental lançada da Terra tem intensidade v A = 32,32 × 10 3k m / h no ponto A , determine a velocidade da sonda quando ela passar pelo ponto B .
Quanta energia por quilograma deve ser fornecida a um satélite a fim de colocá-lo em uma órbita circular a uma altitude de ( a ) 600 k m e ( b )6.000k m ?
Uma sonda espacial descreve uma órbita circular de raio nR com velocidade v0 em torno de uma planeta de raio R e centro O. Mostre que (a) para que a sonda espacial deixar sua órbita e atingir o planet
Usando as respostas obtidas no Problema 13.107, mostre que a órbita circular pretendida e a órbita elíptica resultante interceptam-se nas extremidades do eixo menor da órbita elíptica.