Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 195
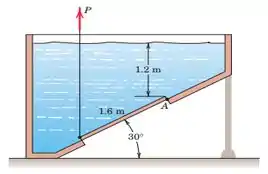
A seção transversal de um tanque de água doce com um fundo inclinado é mostrado. Uma porta retangular de 1,6 m por 0,8 m (normal ao plano da figura) no fundo do tanque é articulado em A e é aberto contra a pressão da água pelo cabo sob uma tensão P, como mostrado. Calcule P.
Passo 1
E ai gurizada tudo belezinha???
Observe que para determinar a força P necessária para abrir a porta, precisaremos calcular a pressão que atua na porta da água.
Observe que a água está sempre agindo normal à superfície, e a expressão para pressão na profundidade h é:
Como a densidade da água é: e gravidade é , podemos escrever a expressão acima como:
No esboço abaixo, podemos ver que os pontos A e B estão em profundidade de:
Assim, podemos calcular as pressões atuando nos pontos A e B.
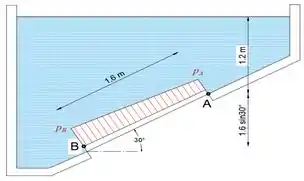
Observe que este é um problema tridimensional, que podemos resolver como bidimensional convertendo a pressão que atua na porta retangular na linha AB. Uma vez que a largura da porta é , pressume-se de toda a largura atuando nos pontos A e B é.
Passo 2
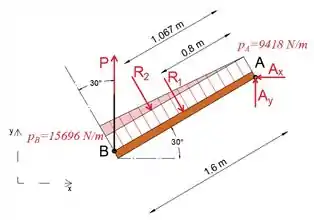
A seguir, isolaremos e desenharemos o diagrama de corpo livre da dor.
Observe que dividimos a camada trapezoidal distribuída em camadas retangulares e triangulares, e substituímos ambas pela resultante, que atua no centro de gravidade do retângulo, ou seja, o triângulo.
Passo 3
Ao igualar a soma dos momentos sobre o ponto A a zero, eliminaremos as forças de reação em A, então o único desconhecido será a força P.
A partir daqui, podemos expressar a força P como:
Substitua por seus valores.
Resposta
- Calculando a expressão acima, obtivemos que a força P exigida para abrir a porta é: