21. Quando se segura uma pedra de em equilíbrio, o úmero , considerado liso, exerce uma força normal e no rádio e no cúbito , como mostra a figura. Determine essas forças e a força que o bíceps exerce sobre o rádio para manter o equilíbrio. A pedra tem centro de massa em . Despreze o peso do braço.
Passo 1
Primeiro, vamos ver o diagrama de forças da nossa situação, para analisar as reações que teremos que determinar no nosso sistema e ficar mãos simples de ver o que fazer.
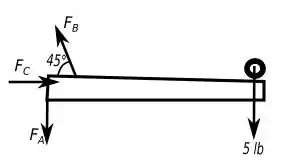
Então para achar as reações que o enunciado pede, teremos que usar as equações de equilíbrio.
Mas será mais conveniente calcular o momento em relação ao ponto , já quee , não interferem no cálculo do momento pois suas linhas de ação passam por .
Vamos considerar o sentido anti-horário como o positivo.
Passo 2
Vamos então calcular o momento em relação a , para acharmos .
Passo 3
Agora vamos analisar as equações de equilíbrio referentes a força primeiro na direção , depois na direção .