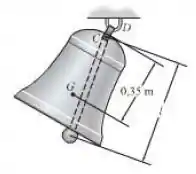
O sino tem uma massa de , um centro de massa em , e um raio de giração em torno do ponto de . O badalo consiste de uma barra delgada fixada à parte de dentro do sino em . Se uma massa de é fixada à extremidade da barra, determine o comprimento da barra, de maneira que o período natural de vibração do badalo seja o mesmo que o do sino. Para o cálculo, despreze a pequena distância entre e e despreze a massa da barra.

Oi pessoal, tudo bem? Vamos analisar essa questão.

Considerando o sentido anti horário positivo, temos:

Podemos considerar para pequenos deslocamentos, portanto:

Temos que:

Como , temos:

Queremos o período que é definido como . Logo:

Podemos fazer a seguinte relação:

Onde o índice diz respeito ao badalo e o índice ao sino.