Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 111

O cilindro de 7,5 Kg está inicialmente em repouso sobre uma placa de 2,5   kg. Se um momento de binário M = 60   N ∙ m for aplicado ao cilindro, determine a aceleração angular do cilindro e o tempo necessário para a extremidade B da placa se deslocar 0,9   m para direita e bater na parede. Suponha que o cilindro não desliza sobre a placa, e despreze a massa dos roletes embaixo da placa.

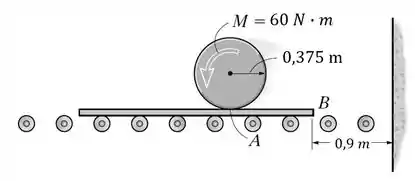
Passo 1

Os diagramas de corpo livre e cinemático do problema em análise são mostrados na figura abaixo:

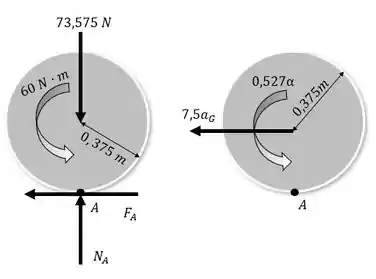
O momento de inércia de massa para o cilindro com a massa concertada no centro pode ser calculado por,

I G = 1 2 m r 2 = 1 2 7,5 0,375 2 = 0,527   k g ∙   m 2

Passo 2

Tendo as informações do DCL e do DC, é possível aplicar 2º lei de Newton para a análise dos corpos

↺ ∑ M A = ∑ M k A

M A = - m a G r G - I G α

- 60 = - 7,5 a G 0,375 - 0,527 α

← ∑ F x = m a G x

F A = 7,5 a G

O DCL da placa sobre os reletes e mostrados na figura abaixo

→ ∑ F x = m a G x

F A = 2,5 a P

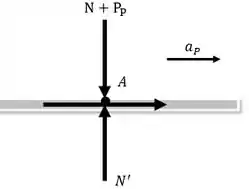
Passo 3

Analisando o movimento do centro de massa do cilindro G e o ponto A , é possível aplicar a seguinte equação cinemática

a G = a A + α × r G / A - ω 2 r G / A

- a G i = a A x i + a A y j + α k × 0,375 j - ω 2 0,375 j

- a G i = a A x + 0,375 i + a A y - 0,375 ω 2 j

Pela componentes i , temos

a G = 0,375 α - a A x

Como os roletes rolam sem deslizar na placa, então a P = a A x . Substituindo em

a G = 0,375 α - a P

Resolvendo o sistema,

- 60 = - 7,5 a G 0,375 - 0,527 α

F A = 7,5 a G

F A = 2,5 a P

a G = 0,375 α - a P

Temos,

α = 75,89   r a d / s 2

F A = 53,36   N

a G = 7,11   m / s 2

a P = 21,34   m / s 2

Passo 4

Para determinar o tempo da extremidade B se deslocar 0,9   m para frete, pode ser calculado por

s = s o + v o t + 1 2 a P t 2

0,9 = 0 + 0 + 1 2 ( 21,34 ) t 2

t = 0,29   s

Resposta

A aceleração angular do cilindro é 75,89   r a d / s 2 o tempo necessário para a extremidade B da placa se deslocar 0,9   m para direita e bater na parede é de 0,29   s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cone maciço de massa m , raio da base r , e altura h está girando a uma taxa elevada p em torno do seu próprio eixo e é liberado com seu vértice O apoiando em uma superfície horizontal. O atrito é s
Um pião constituído por um anel de massa m = 0.52k g e raio médio r = 60m m é montado em um eixo central pontiagudo com raios de massa desprezível. O pião recebe uma velocidade de giro de 10000 r p m
Determine a aceleração a → do ponto A sobre o disco do Prob. 7/135 para a posição mostrada.
Determine a aceleração angular α → para o disco circular que rola do Prob. 7/135. Utilize os resultados fornecidos na resposta para aquele problema.
Determine a velocidade v → do ponto A sobre o disco do Prob. 7/135 para a posição mostrada.