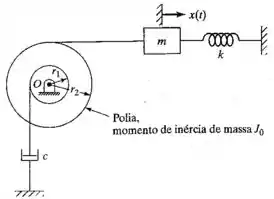
O sistema mostrado na Figura 2.97 tem uma frequência natural de 5 Hz para os seguintes dados: m = 10 kg, J0 = 5 kg/m2, r1 = 10 cm, r2 = 25 cm. Quando o sistema é perturbado por ser-lhe dado um deslocamento inicial, a amplitude de vibração livre é reduzida de 80 por cento em 10 ciclos. Determine o valor de k e c.
Passo 1
E aí pessoal tudo certinho? O enunciado pede que a gente encontre o valor de k e c.
Considere x = deslocamento de massa e P = tensão na corda à esquerda da massa.
Equações de movimento são:
Passo 2
Usando a Eq. (1) em (2) do passo 1obtemos
Com , Eq. (3) pode ser escrito como
Para dados fornecidos, a Eq. (4) torna-se
Passo 3
Uma vez que a amplitude é reduzida em 80% em 10 ciclos,
Uma vez que a frequência natural (assumida como sendo a frequência de vibração torcional não amortecida) é 5 Hz, . Além disso
Assim obtemos: