Um sistema torcional consiste em um eixo com um disco de momento de inercia de massa montado em seu centro. Se ambas as extremidades do eixo forem fixas, determine a resposta do sistema em vibração livre torcional do eixo. Considere que o deslocamento angular inicial disco seja zero e que sua velocidade inicial seja .
Passo 1
E aí, galerinha!
Bom! Bora lá pro que interessa!
Vamos começar fazendo um esboço do nosso sistema pra entender ele um pouco melhor...
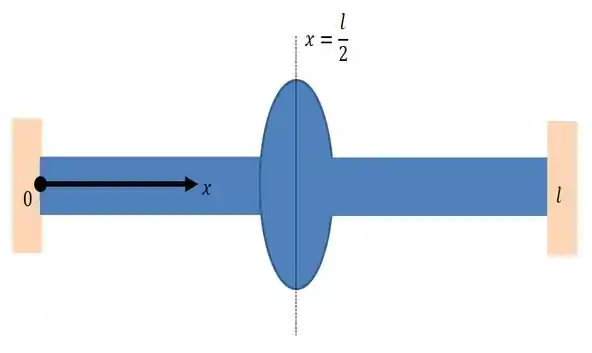
Passo 2
Pois muito bem! Para um sistema torcional, temos a seguinte equação...
E como podemos ver pela nossa figura, onde ambas as extremidades estão fixas... Em , temos que...
Logo, substituindo na equação de :
A melhor chance disso aí dar zero é quando...
Passo 3
Temos também a seguinte equação...
Uma vez que seno dividido pelo cosseno é a tangente...
Baseado na equação de frequência...
Sendo que...
Se as raízes da equação de frequência são dadas por...
Então, baseando na equação para ...
Como sabemos que , então...
Ficamos então, com...
Derivando ...
Multiplicando e por e integrando de até :
Obtemos que...
E ficamos então, com a seguinte equação...