Substitua as cargas dsitribuídas por uma força resultante equivalente e especifique onde sua linha de ação intercepta o elemento , medido a partir de .
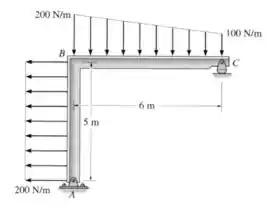
Passo 1
Vamos começar calculando a força total que age sobre o sistema. Para isso temos que calcular a “área” definida por cada uma das distribuições de força.
Começamos pelo trapézio na parte de cima:
Essa força aponta na vertical para baixo.
E agora o retângulo no lado esquerdo:
E essa força aponta na horizontal para a esquerda.
Passo 2
Como essas duas componentes são perpendiculares, o módulo da força resultante será:
E já que essa força é um vetor, vamos encontrar também um ângulo que defina sua direção e sentido.
E como as duas componentes são positivas, esse é o ângulo que o vetor forma com o semieixo horizontal positivo.
Passo 3
Agora vamos calcular o momento resultante dessas forças em relação ao ponto .
Para calcular o momento de uma distribuição de forças, temos que substituí-la por uma força resultante que tenha módulo igual à área da distribuição, e que aja no centroide dessa área.
No caso do retângulo, a área tem módulo , e o centroide fica no centro do retângulo, ou seja, o momento é:
Onde é a distância perpendicular até o ponto :
Para lidar com o trapézio na parte de cima, é útil dividi-lo em duas partes:
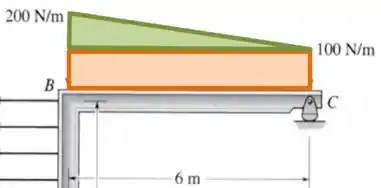
Então:
Já que o centroide do triângulo fica a uma distância igual a um terço do comprimento da base, contando a partir da parte mais alta.
E os dois últimos momentos aparecem com sinal negativo porque favorecem a rotação no sentido horário.
Passo 4
O momento resultante é:
Como queremos o ponto de interseção com o elemento (que é vertical), só precisamos nos preocupar com a componente horizontal da força, e sua distância perpendicular até o ponto :
E só consideramos a componente horizontal da força, porque só ela vai produzir momento em relação ao ponto .
Resposta
As cargas podem ser substituídas por uma força de de intensidade, formando um ângulo de com o semieixo horizontal positivo, e agindo a uma distância de acima do ponto .