Substitua as cargas por uma força e um momento equivalentes que atuam no ponto .
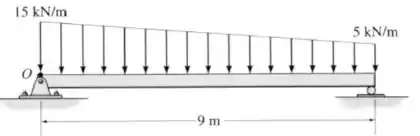
Passo 1
Para calcular a força total gerada pela distribuição, precisamos calcular a área do trapézio que é definido por ela.
Lembrando que, para calcular a área do trapézio, seguimos a seguinte fórmula:
Então:
E essa força aponta na vertical para baixo:
Passo 2
Agora vamos calcular o momento total exercido por esa força em relação ao ponto . Podemos trocar a distribuição de forças por uma única força que tenha módulo igual à área da distribuição, e que aja na direção do centroide dessa área.
Nesse caso é útil dividir a área da distribuição em dois pedaços:
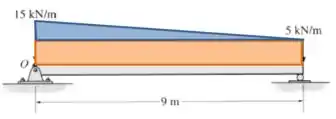
O centroide do retângulo estará na metade do seu lado de , e o centroide do triângulo estará a da altura total () a partir de :
E agora é só substituir as forças pelas áreas de cada figura:
Resposta
Podemos substituir a carga por uma força aplicada em , e um momento .