Substitua as cargas por uma força resultante equivalente e especifique sua localização sobre a viga, medida a partir do ponto .
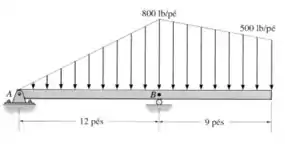
Passo 1
Para calcular a força total gerada por cada uma das distribuições, primeiro precisamos obter as áreas totais das duas figuras.
À esquerda, temos um triângulo de altura e base de , então:
À direita temos um retângulo e um triângulo logo acima dele. Começamos pelo triângulo:
E para o retângulo:
Então a força resultante é:
Na vertical para baixo.
Passo 2
Agora vamos calcular o momento total exercido por essas forças em relação ao ponto .
Podemos tratar cada distribuião como uma força (de módulo igual à área da distribuição), agindo no centroide da figura.
O centroide do triângulo da esquerda está a do ponto :
O centroide do segundo triângulo (o da direita), está a do ponto :
E o centroide do retângulo da direita está a do ponto :
Então o momento resultante é:
Passo 3
Para que a nossa força produza o mesmo momento que tínhamos inicialmente, a distância do seu ponto de aplicação até o ponto deve ser:
Que deve estar à direita do ponto para manter as condições iniciais.
Resposta
Podemos substituir a carga por uma força na vertical para baixo, aplicada à direita do ponto .