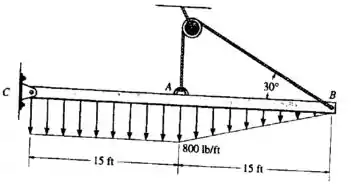
Substitua o carregamento distribuído por uma força resultante equivalente e especifique sua localização sobre a viga, a partir do pino em .
Passo 1
Começamos calculando a força resultante agindo sobre a viga. Para calcular a força associada a cada uma das distribuições, precisamos calcular as áreas das duas figuras formadas por elas:
Então a força resultante é:
Apontando na vertical para baixo.
Passo 2
Agora vamos calcular o momento total dessas forças em relação ao ponto .
O centroide do retângulo está a uma distância:
Do ponto , de forma que o momento gerado pela força de associada a ele produz o seguinte momento:
E o centroide do triângulo está a uma distância:
Então, como a força associado ao triângulo é de :
Então o momento resultante é:
Passo 3
Se queremos substituir a distribuição por uma única força que produz o mesmo momento, a distância dela até o ponto deve ser:
Resposta
Podemos substituir a carga por uma força , agindo a do ponto .