Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 10ª Edição - Russel C. Hibbeler- Ed: 10º - Capítulo 4.10 - Ex. 154

Substitua as cargas por uma força resultante e um momento equivalentes atuantes no ponto O .

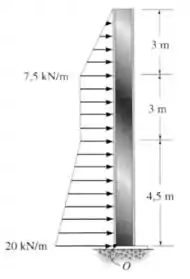
Passo 1

Temos que cumprir duas tarefas para resolver a questão: calcular a força resultante sobre o sistema e calcular o momento resultante em relaçao ao ponto O .

Começamos com a força resultante, para isso só precisamos calcular a área dessa dsitribuição de forças. Para isso vamos dividir a área total em quatro partes:

A l a r a n j a = 1 2 3 7,5 = 11,25   k N

A v e r m e l h a = 3 7,5 = 22,5   k N

A v e r d e = 4,5 7,5 = 33,75   k N

A r o x a = 1 2 20 - 7,5 4,5 = 28,125   k N

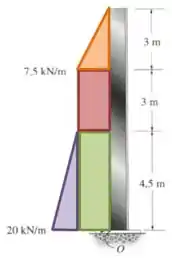
Então a força total é:

∑ F = A l a r a n j a + A v e r m e l h a + A v e r d e + A r o x a

∑ F = 11,25 + 22,5 + 33,75 + 28,125

∑ F ≅ 95,6   k N

Passo 2

Agora, para calcular o momento, vamos mostrar a posição do centroide de cada cada distribuição.

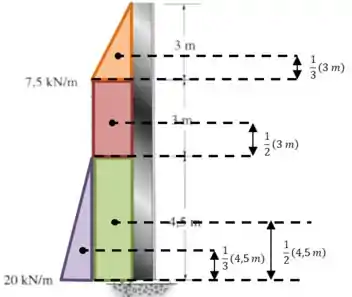
Então o momento resultante é:

∑ M = F l a r 4,5 + 3 + 1 3 3 + F v e r m 4,5 + 1 2 3 + F v e r d 1 2 4,5 + F r o x 1 3 4,5

∑ M = F l a r 8,5 + F v e r m 6,0 + F v e r d 2,25 + F r o x 1,5

∑ M = 11,25 8,5 + 22,5 6,0 + 33,75 2,25 + 28,125 1,5

∑ M = 349   k N ∙ m

E esse momento favorece a rotação no sentido horário em torno de A .

Resposta

As cargas podem ser substituídas por uma força resultante F = 95,6   k N (na horizontal, para a direita) atuando em O e um momento de módulo M = 349   k N ∙ m , atuando no sentido horário.

Ver Outros Exercícios desse livro