Substitua as cargas por uma única força resultante e especifique a localização dessa força sobre a viga, medida a partir do ponto .
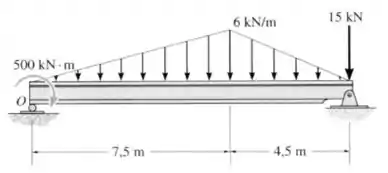
Passo 1
Para encontrar as forças geradas por cada distribuição, vamos calcular as áreas das figuras formadas por elas:
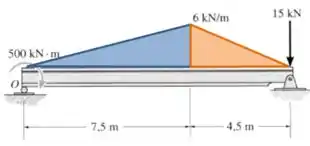
Começamos com a área do triângulo azul:
E agora o triângulo laranja:
E o sinal negativo aparece nas duas forças porque ambas apontam para baixo no eixo vertical. Além delas, temos a força de , que também deve entrar na conta da força resultante:
Passo 2
E agora vamos calcular o momento resultante em relação ao ponto . Começamos pela força de e pelo momento de binário já representado no desenho:
E para encontrar o momento das forças associadas às duas áreas, temos que nos lembrar de que, em cada uma delas, podemos considerar que a força age na direção do centroide de cada área.
E o centroide de um triângulo retângulo está a uma distância de do comprimento da base, em direção ao lado mais alto (naturalmente):
Então:
Onde tomamos o sentido horário como positivo.
Passo 3
Agora temos que escolher a posição da nossa força resultante de forma que o momento total em relação a continue o mesmo.
Então se é a distância perpendicular entre o ponto e o ponto de aplicação da força:
Lembrando que a força precisa estar à direita do ponto , para que o momento resultante aponte no sentido horário, assim como fazia no sistema original.
Resposta
As cargas podem ser substituídas por uma única força atuando a do ponto .