Substitua a força em por uma força e um momento equivalentes no ponto .
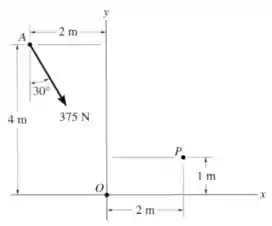
Passo 1
O primeiro passo é calcular o momento da força em , para isso vamos lembrar da definição do momento:
Onde é o vetor posição do ponto em relação à origem:
E também podemos escrever a força em forma vetorial pelas informações do desenho:
Passo 2
Agora vamos resolver o produto vetorial para calcular o momento:
Passo 3
Quando substituirmos a força em por uma força igual aplicada no ponto , o momento em relação a será nulo.
Então, se quisermos fazer essa substituição sem mudar o resultado final sobre o sistema, precisamos acrescentar um momento em igual ao que tínhamos antes de substituir a força:
E a força continuará tendo a mesma expressão, já que a forma de um vetor não depende do seu ponto de aplicação:
Resposta
A força em pode ser substituída por um par formado por uma força em , e um binário