Substitua o sistema de forças por uma força e um momento equivalentes no ponto .
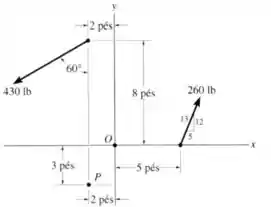
Passo 1
Vamos começar calculando a força resultante que age sobre o sistema. Para isso, primeiro precisamos escrever cada uma das forças em forma vetorial.
Começando pela força da direita. Para encontrar o ângulo, podemos tirar proveito daquele triângulo retângulo desenhado ao lado do vetor:
Então:
E agora fazemos o mesmo paa a força da esquerda:
Então a força resultante é:
Passo 2
Podemos definir essa força a patir de um módulo e um ângulo:
Já que estamos trabalhando com um vetor que tem uma coordenada negativa em , vai ser o ângulo que ele forma com o semi-eixo horizontal negativo:
Beleza, já temos a força que vai substituir o par representado no desenho, falta alpicar um binário que substitua o momento que as duas forças originais tinham em relação ao ponto .
Passo 3
Para calcular o momento de cada força vamos desenhar suas componentes em cada eixo:
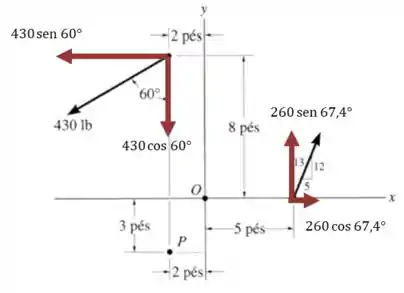
E então temos que multiplicar cada componente pela sua distância perpendicular até o ponto . Começando pela força da direita:
Lembrando de que o sinal negativo aparece nas componentes que favorecem rotação no sentido horário (em torno de ).
E para a força da esquerda:
E então o momento resultante é:
Que também pode ser escrito como:
Já que .
Resposta
O sistema pode ser substituído por uma força aplicada em , formando um ângulo de com o semieixo horizontal negativo, e por um binário .