Substitua o sistema de forças por uma única resultante e especifique seu ponto de aplicação, medido ao longo do eixo a partir do ponto .
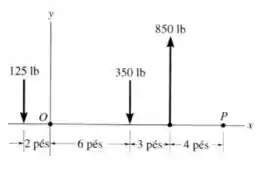
Passo 1
Vamos começar escrevendo cada uma das forças do desenho em forma vetorial:
Então a força resultante é:
Para descrever essa força como um vetor, vamos achar seu módulo e ângulo de inclinação.
Como o vetor é totalmente vertical, sabemos que ele forma um ângulo de com o semi-eixo horizontal positivo:
Passo 2
Se nós vamos substituir essas três forças por uma única força aplicada em um ponto qualquer, o momento dessa nova força em relação a esse ponto vai se anular.
Para que o resultado final continue o mesmo depois de fazermos a substituição, vamos ver qual era o momento total das forças em relação ao ponto inicialmente.
Temos que multiplicar cada uma das forças pela sua distância perpendicular até o ponto , colocando um sinal negativo naquelas que favorecem a rotação no sentido horário.
Beleza, esse também tem quer se o momento da nossa nova força em relação ao ponto .
Entãpo, se a força está a uma distância perpendicular do ponto , ela tem que obedecer a seguinte relação:
Resposta
O sistema pode ser substituído por uma única força a do eixo horizontal (sentido anti-horário), localizada a pés do ponto , ao longo do eixo .