O suporte, a bigorna e a base do martelo de forjar mostrados na Figura 4.37(a) têm uma massa total O coxim elástico de apoio tem uma rigidez . Se a força aplicada pelo martelo for dada pela Figura , determine a resposta da bigorna.
Passo 1
Partiu determinar a resposta da bigorna
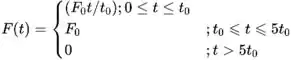 (E1)
(E1)
Resposta da bigorna é dada por para um sistema sem amortecimento
(E2)
Para
(E3)
Passo 2
Para
(E4)
Passo 3
Para :
(E5)