Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 124

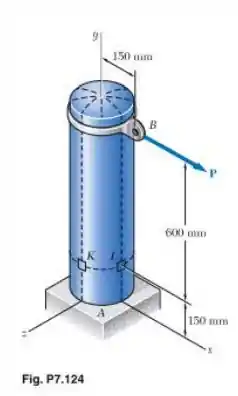
O tanque de ar comprimido A B   tem um diâmetro externo de 250   m m   e espessura de parede de 8   m m .   Ele é equipado com um anel no qual é aplicada uma força P   de 40   k N   horizontal em B .   Sabendo que a pressão manométrica no tanque é de 5   M P a ,   determine a tensão normal máxima e a tensão de cisalhamento máxima no ponto K .

Passo 1

Fala aí, galerinha. Tudo bem com vocês? Vamos para outra questão.

Primeiro, sabemos que a pressão é:

p = 5   M P a = 5 × 10 6   M P a

Para um tubo de paredes finas, a tensão axial e radial são, respectivamente:

σ x = p r t

σ y = p r 2 t

Substituindo os valores:

r = 1 2 d - t = 117   m m

σ x = 73,125   M P a

σ y = 36,563   M P a

Passo 2

Como o ponto K   está na linha neutra, temos que:

σ y = 0

Logo, teremos a tensão causada pelo cortante. Ela é dada por:

τ x y = V Q I t

Onde V   é o cortante, Q   é o momento estático, t   é a espessura e I   o momento de inércia. Calculando os parâmetros:

Q = 2 3 r e x 3 - r i n   3 = 134,34 × 10 - 6   m 3

I = π 4 r e x 4 - r i n   4 = 44,573 × 10 - 6   m 4

Logo:

τ x y = V Q I t = 13,1436   M P a

Passo 3

Portanto, temos o seguinte estado de tensões:

σ x = 73,125   M P a

σ y = 36,563   M P a

τ x y = 13,1436   M P a

Logo, a tensão média será:

σ m é d = 1 2 σ x + σ y = 54,844   M P a

O raio é dado por:

R = σ x - σ y 2 2 + τ x y 2 = 22,516   M P a

Logo, a tensão máxima é dada por:

σ m á x = σ m é d + R = 77,4   M P a

Já a mínima:

σ m í n = 0

Passo 4

Por fim, a tensão máxima cisalhante será dada por:

τ m á x = 1 2 σ m á x - σ m í n = 38,7   M P a

Resposta

σ m á x = 77,4   M P a

τ m á x = 38,7   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um anel de latão com diâmetro externo de 127m m e espessura de 6,35m m se encaixa exatamente dentro de um anel de aço com diâmetro interno de 127m m e 318m m de espessura, quando a temperatura de ambo
O tanque mostrado tem um diâmetro interno de 180m m e uma espessura de parede de 12m m . Sabendo que ele contém ar comprimido sob pressão de 8M P a , determine a intensidade T do torque aplicado para
Um reservatório de gás esférico feito de aço tem um diâmetro externo de 6096 mm e parede com espessura de 11,1 mm. Sabendo que a pressão interna é de 517,1 kPa, determine a tensão normal máxima e a te
O tanque de armazenamento mostrado na Foto 7.3 tem um diâmetro externo de 3,3 m e uma espessura de parede de 18 mm. Quando a pressão interna do tanque for 1,5 MPa, determine a tensão normal máxima e a