Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 123

O tanque mostrado tem um diâmetro interno de 180   m m   e uma espessura de parede de 12   m m .   Sabendo que ele contém ar comprimido sob pressão de 8   M P a ,   determine a intensidade T   do torque aplicado para o qual a tensão normal máxima é de 75   M P a .

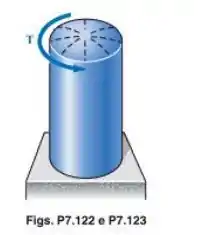
Passo 1

Fala aí, galerinha. Tudo bem com vocês? Partiu outra questão.

Primeiramente, temos os seguintes parâmetros fornecidos:

d = 180   m m → r 1 = 90   m m

t = 12   m m

Onde t   é a espessura da parede e este raio é o interno. O raio externo será o raio interno mais a espessura, logo:

r 2 = 90 + 12 = 102   m m

Com isso, como a tensão cisalhante gerada pelo momento depende do momento polar de inércia da seção, podemos calculá-lo:

J = π 2 r 2 4 - r 1 4

J = 66,968 × 10 6   m m 4

Passo 2

Sabemos que, para um tubo de paredes finas, a tensão normal axial e radial são dadas por:

σ 1 = p r t

σ 2 = p r 2 t

Onde t   é a espessura da parede, p   é a pressão interna e r   é o raio interno. Logo, substituindo:

σ 1 = 60   M P a

σ 2 = 30   M P a

Passo 3

Agora, devemos usar os parâmetros do círculo de Mohr. Calculando a tensão média:

σ m é d = 1 2 σ x + σ y

σ m é d = 45   M P a

A tensão máxima fornecida pelo problema é de 75   M P a .

Este é o centro do nosso círculo de Mohr. O raio é dado por:

R = σ m á x - σ m é d = 30   M P a

Por último, a tensão cisalhante será:

τ x y = R ² - σ 1 - σ 2 2 2

Logo:

τ x y = 25,98   M P a

Passo 4

Agora, podemos calcular o torsor pela fórmula da tensão cisalhante devido a torsão. Ela será:

τ = T c J

Logo:

T = J τ x y c

Substituindo:

T = 17,06   k N m

Resposta

T = 17,06   k N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o tanque de armazenagem do Problema 7.104, determine a tensão normal máxima e a tensão de cisalhamento máxima na parede cilíndrica quando o tanque estiver totalmente cheio (h = 14,5 m).
Um tubo de aço padrão pesado com 12 in. de diâmetro nominal suporta água sob pressão de 400 psi. (a) Sabendo que o diâmetro externo é de 12,75 in. e que a espessura da parede é de 0,375 in., determine
Um tanque de armazenamento contém propano líquido sob uma pressão de 1,5 MPa, a uma temperatura de 38 °C. Sabendo que o tanque tem um diâmetro externo de 320 mm e espessura de parede de 3 mm, determin
Um tubo de aço com diâmetro externo de 12 in. é fabricado a partir de uma chapa de espessura igual a 1/4 in. soldada ao longo de uma hélice que forma com o plano perpendicular ao eixo do tubo um ângul
Para o tanque de ar comprimido e o carregamento do Prob. 7.165, determine a tensão normal máxima e a tensão de cisalhamento máxima no plano no ponto b no topo do tanque.