Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 58
Trace os diagramas de cortante e momento fletor para a viga e o carregamento mostrado, e determine a tensão normal máxima provocada pelo momento fletor.
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora pra outra questão pra ficarmos craques na matéria.
O primeiro passo é determinar a reação de apoio, para que possamos fazer os diagramas. O DCL será:
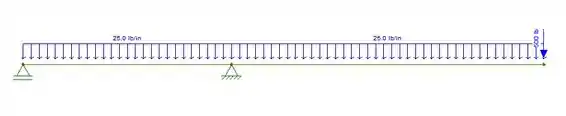
Aplicando as equações de equilíbrio:
Passo 2
Agora, com as reações calculadas, podemos fazer os diagramas pedidos. O diagrama de cortante será:
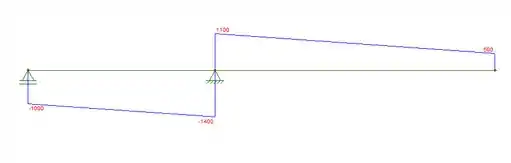
Já o diagrama de momento fletor, será:
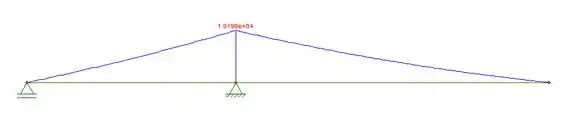
Tomem cuidado porque as unidades desse problema não estão no SI, elas são unidades americanas.
Passo 3
Agora, vamos determinar a tensão normal máxima. A tensão normal é dada por:
Onde é o momento fletor e é uma propriedade da seção, que é tabelada. Pegaremos o momento máximo para achar a tensão máxima, para isso, basta olhar no diagrama de momento.
Para este caso, utilizando os ábacos do fim do livro, temos que:
A tensão máxima, para este caso, será:
Prontinho, encontramos a tensão pedida.