Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 4
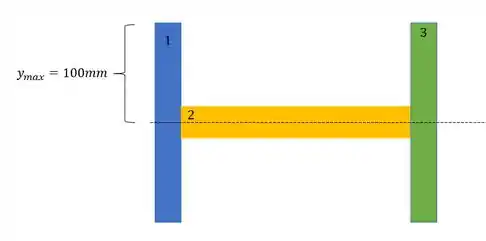
Resolva o , admitindo que a viga de mesa larga é fletida em relação ao eixo por um conjugado de momento .
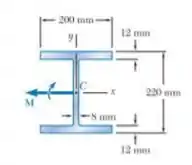
Passo 1
Fala galerinha, nosso objetivo com essa questão é determinar o momento máximo que podemos aplicar na nossa estrutura, para isso temos que saber a máxima tensão que age nela.
Então temos que lembrar que a nossa fórmula de tensão quando temos um momento agindo é dada por:
E cada terminho desse é bem tranquilo de determinar, beleza? Então vamos lá.
Passo 2
Existem dois termos que não dependem em nada dos pontos aplicado, então vamos determinar eles primeiro, já que são comuns aos dois:
- (tensão admissível, ou tensão máxima)
- I (momento de inércia)
Essa o enunciado da de graça pra gente, assim temos que:
E como queremos saber o momento máximo que age, temos que fazer a seguinte igualdade:
Agora para fazermos esse momento de inércia precisamos fazer uma separação da nossa estrutura em estrutura mais simples, e olha, um macete legal é dividir em retângulos porque já sabemos que a fórmula para retângulos é dada por:
Sabendo disso, podemos dividir a nossa seção em seções mais simples, mas ainda mais, além disso, podemos girar a nossa seção para facilitar a conta, assim teremos que:
Como todas as estruturas tem o centroide compatível com o centroide da peça como um todo, teremos que:
Agora só precisamos do y e para termos o momento máximo, precisamos de um ponto especifico.
Passo 3
Para termos o momento máximo, precisamos do y mais distante da LN, porque assim teríamos a tensão máxima que age na nossa seção, e por consequência, teremos o momento máximo, dessa forma, teremos que usar o valor com relação a y, assim teremos que:
