Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 69
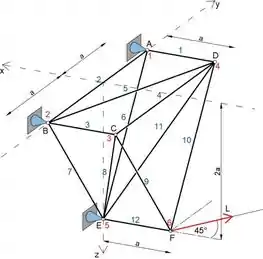
A treliça espacial mostrada é presa aos suportes fixos em A, B e E e é carregada pela força L que tem componentes xey iguais, mas nenhum componente z vertical. Mostre que há um número suficiente de membros para proporcionar estabilidade interna e que sua colocação é adequada para esse fim. Em seguida, determine as forças nos membros CD, BC e CE.
Passo 1
Verificaremos se a treliça é estaticamente determinada internamente pela equação abaixo
Onde m é um número de membros e j número de juntas. Esta treliça contém seis juntas e doze membros
Uma vez que a equação é satisfeita e cada junta tem pelo menos três membros conectados, isso significa que a treliça é determinada estaticamente
Podemos ver que existem três forças desconhecidas agindo no ponto F, portanto, analisando a junta F, podemos determinar a força CF
Podemos notar que a força FE é paralela ao eixo x, então podemos escrevê-la como
Enquanto a força L está fazendo um ângulo de 45∘ com eixo x negativo para que possamos escrevê-lo como
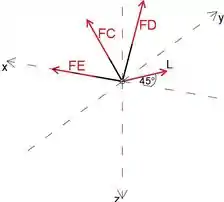
Podemos escrever o vetor de força FC como um produto de sua magnitude CF e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos F e C são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Passo 2
Podemos escrever o vetor de força FD como um produto de sua magnitude DF e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos F e D são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Agora que escrevemos todas as forças como vetores, podemos escrever três equações de equilíbrio igualando a soma das forças a zero
Agora temos 3 equações de equilíbrio
(1)
(2)
(3)
Podemos multiplicar a equação (2) por
(4)
Ao adicionar as equações (3) e (4), obteremos uma equação com apenas uma incógnita
Passo 3
Podemos notar que agora existem três forças desconhecidas agindo no ponto C, então, analisando a junta C, podemos determiná-las
Presumimos que todos os membros estão em tensão
Podemos notar que as forças CB e CD são paralelas aos eixos xey respectivamente, então podemos escrevê-las como
Observe que o vetor é oposto ao vetor
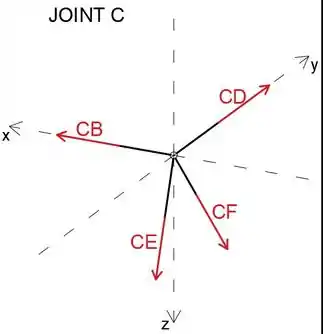
Passo 4
Podemos escrever o vetor de força como um produto de sua magnitude CE e um vetor unitário de direção de força
Podemos ver na imagem que as coordenadas dos pontos C e E são
Uma vez que conhecemos dois pontos na linha de ação, podemos escrever como
Agora que escrevemos todas as forças como vetores, podemos escrever três equações de equilíbrio igualando a soma das forças a zero
Agora temos 3 equações de equilíbrio
(5)
(6)
(7)
Da equação (7) podemos determinar a força no membro CE
Como obtivemos resultado negativo, isso significa que o membro CE está em compressão
Podemos substituir a força CE na equação (5) por seu valor para determinar a força BC
Finalmente, podemos substituir a força CE na equação (6) por seu valor para determinar a força CD