65- A treliça espacial é utilizada para sustentar forças verticais nos nós e . Determine as forças em cada um dos elementos e indique se eles estão sob tração ou compressão.
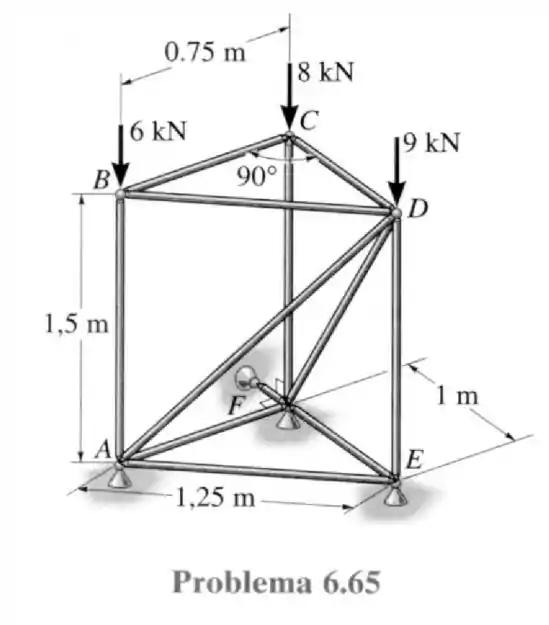
Passo 1
Vamos traçar eixos coordenados nas juntas da estrutura e assim ser capaz de dizer o quanto de esforço cada barra faz. Começando pela junta :
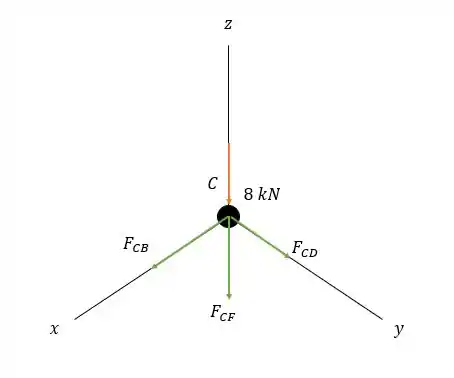
Fazendo a somatórias das forças em nós teremos:
Força compressiva, pois da forma que está representado a força no desenho (saindo do nó,entrando na barra) o sinal negativo representa uma força compressiva e a positiva uma força trativa.
Fazendo a somatória da forças em temos:
Agora fazendo a somatória das forças em :
Passo 2
Agora vamos para avançar para o nó .
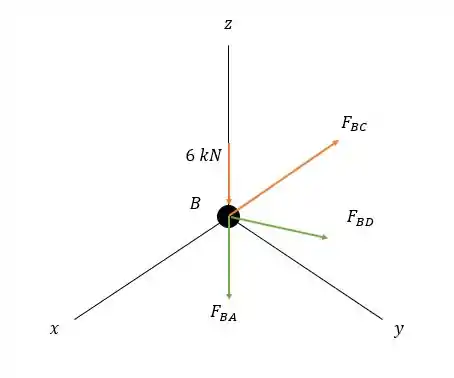
Como está no plano e como nesse plano não há nenhuma força agindo então:
E pela somatória das forças em :
Passo 3
Agora avançando para a junta temos a barra que tem componentes em e apenas, fazendo a somatória das forças em teremos:
E a barra tem componentes em , e e por conta disso a somatória das forças em dessa barra nos daria:
O que sobra a barra que pela somatória das forças em nos daria:
Passo 4
Agora para as juntas e só nos sobraram barras que estão em planos e e como não forças ativas nesses eixos logo não haverão forças reativas também.