Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas Fundamentais - Ex. 30
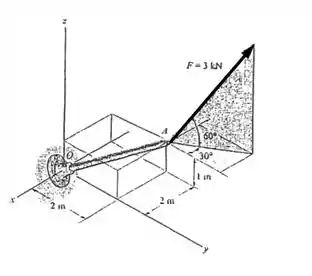
Determine as componentes da força que atuam paralela e perpendicular ao eixo da barra.
Passo 1
Falaa, aí! Ele quer a intensidade das componentes das forças na direção paralela a barra e na linha perpendicular a ela.
O que ele quer dizer é que queremos projetar a força nessa barra e achar sua intensidade (seu módulo) e fazer o mesmo para a linha perpendicular a . Falou de projetar, cê lembra logo de produto escalar!
Como aqui a gente está em 3D, fica mais tranquilo usarmos formulação de vetor cartesiano, tá bem?
Então, a gente precisa escrever a força como um vetor e o nosso eixo da barra como vetor unitário e fazer o produto escalar entre eles.
Vem ver como fica!
Passo 2
Desejamos calcular as componentes da força que atuam paralela e perpendicular ao eixo da barra, para isso vamos primeiramente escrever em termos dos vetores que representam os eixos , respectivamente. Dessa forma, vamos fazer nossa colinha de decomposição de vetores da seguinte forma
Agora, vamos atrás de cada uma das componentes do nosso vetor. Para os eixos precisamos da força decomposta no plano usando o depois ajustá-la com relação ao ângulo de . Começando para a componente temos
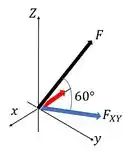
Primeiro vamos decompor no vetor azul e depois no vermelho, sendo assim temos
Agora, decompondo o vetor azul em relação ao vermelho
Porém, como a componente está para o lado negativo do eixo vamos colocar um sinal de negativo nela, obtendo então . Agora, vamos para o eixo procedendo da mesma forma vamos decompor da seguinte forma
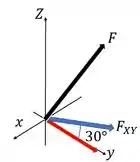
Nesse caso, teremos
Agora, decompondo o vetor azul em relação ao vermelho
Por fim, para a componente a decomposição é mais simples basta encontrarmos o valor de (segundo a nossa cola, ele é o eixo vertical) que será dado por
Juntando todos os nossos componentes obteremos o seguinte
Passo 3
Tendo o vetor vamos calcular, agora, o vetor unitário que sai de e vai para que aqui chamaremos de . Achamos esse vetor fazendo a coordenada final menos inicial. Aí o vetor unitário será dado pela divisão do vetor
pelo seu módulo então, temos
Passo 4
Agora que a gente tem o vetor da força e o vetor unitário na direção de , a gente acha a intensidade da força projetada na direção de fazendo o produto escalar entre esses vetores:
Lembrando que o produto escalar é feito termo a termo semelhante.
Passo 5
Para achar a componente perpendicular, vamos pensar assim. Com duas componentes e perpendiculares entre si de uma força, a gente consegue achar o módulo dessa força fazendo
No nosso caso, temos duas componentes perpendiculares entre si, que a gente achou e a que a gente quer achar , que está na direção normal a . E elas são componentes de . Aí temos
Aí a gente pode isolar e achar:
Pronto, está resolvido nosso problema. Até que foi fácil, né? rs
