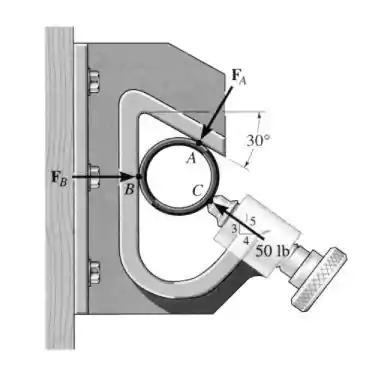
O tubo é mantido na posição pela morsa. Se o parafuso exerce uma força de sobre o tubo na direção mostrada, determine as forças e que os contatos lisos em e exercem sobre o tubo.
Passo 1
Esse problema proposto pelo enunciado é um problema bidimensional. Para encontrarmos o que é pedido no enunciado, temos que analisar a situação em equilíbrio, logo:
Mas para isso, teremos que decompor a força exercida pelo parafuso e a força . A força facilitou a nossa vida, já que ela tem a mesma direção de , logo ela só tem componente nessa direção.
Mas como vamos decompor as forças do parafuso e a ? Bem, cada uma vai ser de uma forma, vamos começar primeiro com .
Passo 2
Se repararmos a figura, podemos notar que sofre uma inclinação de com a vertical, logo suas componentes em e , são:
Agora vamos ver a força do parafuso.
Se você reparar tem um triangulo retângulo desenhado nela, isso é uma maneira de indicar proporcionalidade, logo a componente dessa força vale e a componente vertical vale . Assim,
Agora que temos essas informações vamos analisar as equações de equilíbrio que temos mais acima.
Passo 3
Abrindo as equações de equilíbrio temos:
E considerando que para a direita será o nosso positivo:
E no eixo vertical, considerando para cima positivo:
Passo 4
Do passo , achamos o seguinte;
Vamos substituir a primeira equação na segunda, para acharmos .