Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 13.Problemas - Ex. 92
O tubo tem 6 mm de espessura, é feito de liga de alumínio 2014-T6 e está engastado nas extremidades. Determine a maior carga axial que ele pode suportar.
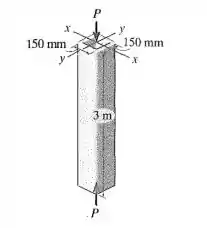
Passo 1
Como está engastado nas extremidades,
Calculando-se o momento de inércia e a área, teremos:
Podemos agora determinar o valor de
Agora, vamos verificar se o nosso índice de esbeltez satisfaz a condição:
Logo, satisfaz a condição.
Passo 2
Sabemos que a fórmula da tensão admissível é:
E sabemos que:
Portanto:
Isolando-se o , teremos:
Resposta
Exercícios de Livros Relacionados
Quatro pranchas de madeira, cada uma de 38x190mm de seção transversal, são firmemente pregadas juntas,como mostrado, para formar uma coluna. Sabendo-se que para o tipo de madeira usadoE=12GPa e que a
Uma coluna de comprimento efetivo igual a 6m é obtida pela conexão de dois perfislaminados de aço C180X14,6, como indicado. Sabendo-se que σ e =250MPa e E=200GPa, determinar a carga admissível para a
Quatro pranchas de madeira, cada uma de 38x190mm de seção transversal, são firmemente pregadas juntas,como mostrado, para formar uma coluna. Sabendo-se que para o tipo de madeira usadoE=12GPa e que a
Quatro pranchas de madeira, cada uma de 38x190mm de seção transversal,são firmemente pregadas juntas, como mostrado, para formar uma coluna. Sabendo-seque para o tipo de madeira usada E=12GPa e que a
Quatro pranchas de madeira, cada uma de 38x190mm de seção transversal, são firmemente pregadas juntas,como mostrado, para formar uma coluna. Sabendo-se que para o tipo de madeira usadoE=12GPa e que a