Usando o círculo de Mohr, demonstre que a expressão , é independente da orientação dos eixos e , onde , e , representam , respectivamente, os momentos e o produto de inércia de uma superfície em relação a um par de eixos retangulares e passando por um dado ponto . Mostre também que a expressão dada é igual ao quadrado do comprimento da tangente traçada da origem do sistema de coordenadas ao círculo de Mohr.

Oi pessoal, tudo bem? Vamos analisar essa questão.

O circulo de Mohr abaixo desmonstra a situação:

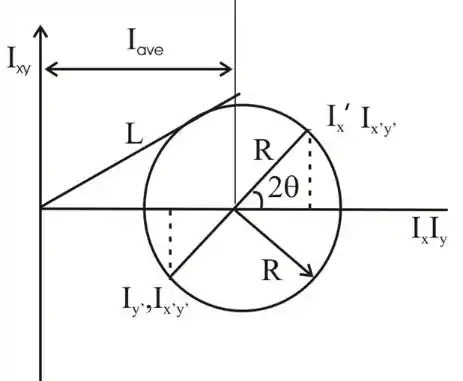
Temos que:

Para demonstrar , vamos substituir as relações acima:

Como é constante, temos que é independente do ângulo do eixo.

Podemos observar também que a tangente , analisando geometricamente, pode ser tratada como:

E como:

Temos que: