Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 126
Se o peso por unidade de comprimento do cabo é , prove que a curva formada pelo cabo é um arco de círculo. (Dica: use a propriedade indicada no Problema ).
Passo 1
Bom galera, vamos fazer um diagraminha de corpo livre bem simples, só pra facilitar nossa vida:
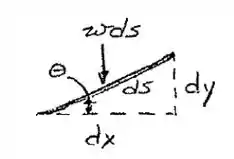
A carga exercida é:
Onde, sabemos que:
Então, substituindo e simplificando, ficamos com:
Passo 2
Show de bola, aplicando a propriedade do Problema , a gente fica com:
Generalizando fica:
Assim, podemos obter:
Que é uma constante.
Pronto, viu como foi até fácil provar isso?
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Para a viga mostrada na figura, determine (a) a intensidade P das duas forças direcionadas para cima para que o valor absoluto máximo do momento fletor na viga é o menor possível, (b) o valor correspo
A viga uniforme é levada por cabos de guindaste ligados em A e B. Determine a distância a das extremidades da viga ate os pontos onde os cabos devem ser ligados se o máximo valor absoluto do momento f
Duas cargas estão suspensas no cabo A B C D tal como mostra a figura. Sabendo que h B = 1,8m , determine a a distância h C , b os componentes da reação em D , c a tração máxima do cabo.
Resolva o Problema 7.60 considerando que P = 1350N e Q = 675N ..
Se d C = 2,4m , determine a a reação A , b a reação E .