Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 104

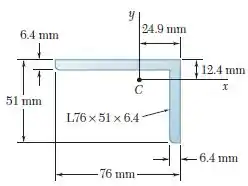
Usando o círculo de Mohr para a seção transversal de cantoneira mostrada na figura, determine a orientação dos eixos centroidais principais e os valores correspondentes do momento de inércia. (As propriedades da seção transversal são dadas na Fig. 9.13).

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

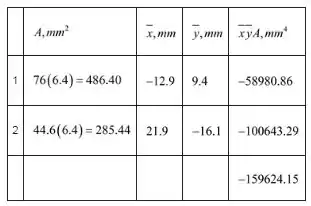
Para obtermos o produto de inércia da seção transversal dada, temos que:

I x y = I x y 1 + I x y 2

Em seguida, temos os produtos de cada retângulo da superfície dada:

I x y = I x ' y ' + x - y - A

Sabemos que há simetria em:

I x y = 0

Passo 2

Portanto, teremos que:

I x y = ∑ x - y - A

I x y = - 0,1596 × 10 6   m m 4

Passo 3

Agora, usando o círculo de Mohr, determinaremos o produto de inércia I x y da superfície dada juntamente com os dados fornecidos na questão:

I m é d = 1 2 I x + I y

I m é d = 1 2 0,162 + 0,454 × 10 6

I m é d = 0,3080 × 10 6   m m 4

Passo 4

O raio do círculo de Mohr será:

R = I x - I y 2 2 + I x y 2

R = 0,162 - 0,454 2 2 + - 0,159584 2 × 10 6   m m 4

R = 0,21629 × 10 6   m m 4

Passo 5

Usando o círculo de Mohr, determinaremos a orientação dos eixos principais.

tan ⁡ 2 θ m = - 2 I x y I x - I y

tan ⁡ 2 θ m = - 2 - 0,159584 × 10 6 0,162 - 0,454 × 10 6

2 θ m = - 47,545 °

E:

θ m = - 23,8 °

Passo 6

Portanto, podemos afirmar que os eixos principais são obtidos por rotação dos eixos x e y em torno de C a 23,8 ° no sentido horário.

Portanto, os momentos principais máximos e mínimos serão:

I m á x , m í n = I m é d ± R

I m á x , m í n = 0,3080 × 10 6 ± 0,21629 × 10 6

Logo:

I m á x = 0,524 × 10 6   m m 4

I m í n = 0,0917 × 10 6   m m 4

Resposta

θ m = - 23,8 °

I m á x = 0,524 × 10 6   m m 4

I m í n = 0,0917 × 10 6   m m 4

Ver Outros Exercícios desse livro