Usando o círculo de Mohr para a superfície indicada, determine a orientação dos eixos centroidais principais e os valores correspondentes dos momentos de inércia.
Superfície do Problema .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Do Problema temos os seguintes momentos de inércia e produto de inércia:
Analisando o círculo de Mohr, que é definido pelo diâmetro , temos que:
E:
A partir disso, podemos achar o momento de inércia do ponto médio do círculo de Mohr. Temos que:
Passo 2
O raio do círculo de Mohr será:
Passo 3
Podemos encontrar a partir de:
E:
Passo 4
Vamos usar o círculo de Mohr para determinar a orientação dos eixos principais na origem e os valores correspondentes dos momentos de inércia em relação a novos eixos obtidos por rotação dos eixos e em torno de de no sentido horário:
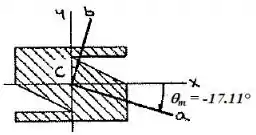
Logo:
E:
Portanto, podemos concluir que no círculo de Mohr é visto que é oo eixo que corresponde a e o eixo corresponde a .
Resposta
E:
Portanto, podemos concluir que no círculo de Mohr é visto que é oo eixo que corresponde a e o eixo corresponde a .