Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 43

Determine por integração direta os centroides das áreas a seguir. Determine a resposta em termos de a e b .

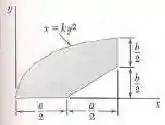
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos o seguinte diagrama:

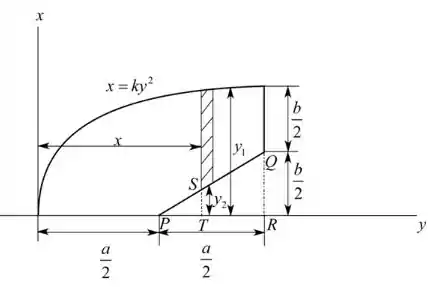
Vamos considerar a parte 0 ≤ x ≤ a 2 e determinar sua área:

A 1 = ∫ 0 a 2 y 1 d x

Temos que:

x = k y 2

k = x y 2

Quando x = a e y = b , temos:

k = a b 2

Logo:

y 1 = x k

y 1 = b x a

Passo 2

Agora vamos analisar a parte a 2 ≤ x ≤ a e determinar sua área:

A 2 = ∫ a / 2   a y 1 - y 2 d x

Analisando o aspecto geométrico podemos dizer que:

y 2 x - a 2 = b 2 a 2

Logo:

y 2 = b a x - a 2

Passo 3

A área total da figura será:

A = A 1 + A 2

A = ∫ 0 a 2 y 1 d x + ∫ a / 2   a y 1 - y 2 d x

Substituindo as equações, temos:

A = ∫ 0 a 2 b x a d x + ∫ a / 2   a b x a - b a x - a 2 d x

Resolvendo, temos que:

A = b a 2 3 x 3 / 2   0 a 2 + b 2 3 x 3 2 a - x 2 2 a + 1 2 x a 2 a

A = 2 3 b a a 2 3 / 2 + b 2 3 a 3 / 2   a - a 2 2 a + 1 2 a - b 2 3 a 2 3 / 2 a - a 2 2 2 a + 1 2 a 2

A = a b 3 + 2 3 a b - a b 2 + a b 2 - a b 3 - a b 8 + a b 4

Portanto:

A = 13 24 a b

Passo 4

Determine o valor do primeiro momento da área usando a seguinte equação:

Q y = ∫ x - e l d A

Q y = ∫ 0 a 2 x - 1 y 1 d x + ∫ a / 2   a x - 2 y 1 - y 2 d x

Os centroides são iguais nos intervalos, então:

x - 1 = x - 2 = x

Portanto, teremos:

Q y = ∫ 0 a 2 x b x a d x + ∫ a / 2   a x b x a - b a x - a 2 d x

Resolvendo, temos que:

Q y = b a 2 5 x 5 / 2   0 a 2 + b 2 5 x 5 / 2 a - x 3 3 a + x 2 4 a 2 a

Q y = 2 5 b a a 2 5 2 + b 2 5 a 5 / 2   a - a 3 3 a + a 2 4 - b 2 5 a 2 5 / 2 a - a 2 3 3 a + a 2 2 4

Q y = a 2 b 5 2 3 / 2 + 2 5 a 2 b - a 2 b 3 + a 2 b 4 - a 2 b 5 2 3 2 + a 2 b 24 - a 2 b 16

Portanto:

Q y = 71 240 a 2 b

Passo 5

Temos também que:

Q x = ∫ y - e l d A

Q x = ∫ 0 a 2 y - 1 y 1 d x + ∫ a / 2   a y - 2 y 1 - y 2 d x

Sabemos que:

y - 1 = y 1 2

y - 1 = b 2 x a

E:

y - 2 = y 2 + y 1 - y 2 2

y - 2 = y 2 + y 1 2

y - 2 = 1 2 b x a + b x a - 1 2

Portanto, teremos:

Q x = ∫ 0 a 2 b 2 x a b x a d x + ∫ a / 2   a 1 2 b x a + b x a - 1 2 b x a - b a x - a 2 d x

Resolvendo, temos que:

Q x = b 2 2 a 1 2 x 2   0 a 2 + b 2 2 x 2 2 a - 1 3 a x a - 1 2 3 a 2 a

Resolvendo, temos que:

Q x = 11 48 a b 2

Passo 6

Agora é só aplicar. Temos que:

x - = Q y A

x - = 71 240 a 2 b 13 24 a b

Portanto:

x - = 71 130 a

Aplicando:

y - = Q x A

Temos que:

y - = 11 48 a b 2 13 24 a b

Portanto:

y - = 11 26 b

Sendo assim o centroide representado por:

x - ,   y - = 71 130 a , 11 26 b

Resposta

x - ,   y - = 71 130 a , 11 26 b

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cabo pesando 25 newtons por metro de comprimento é suspenso do ponto A e passa sobre a pequena polia em B. Calcule a massa m do cilindro acoplado que produzirá o afundamento de 9 m. Determine també
O planador A está sendo rebocado em vôo nivelado e está a 400 pés atrás e 100 pés abaixo do plano de reboque B. A tangente ao cabo do planador é horizontal. O cabo pesa 0,5 lb por pé de comprimento. C
A viga I suporta a força de 1000 lb e o par de 2000 lb-ft aplicado ao suporte de 2 pés soldado na extremidade da viga. Calcule o cisalhamento V e o momento M na seção intermediária entre A e B.
O cabo de massa desprezível é suspenso nos dois pontos fixos mostrados, e a tensão no suporte inferior é suficiente para manter a inclinação zero do cabo naquele ponto. O cabo suporta uma carga unitár
Uma luminária está suspensa no teto de um pórtico externo. Quatro correntes, duas das quais são mostradas, evitam o movimento excessivo do aparelho durante condições de vento. Se as correntes pesarem