Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 42

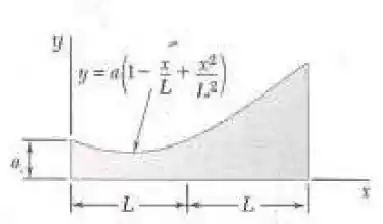
Determine por integração direta o centroide da área mostrada na figura.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Temos o seguinte diagrama:

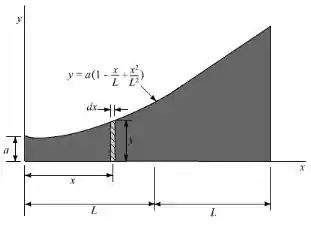
Analisando o elemento diferencial, temos que o seu centroide é dado por:

x - e l = x

y - e l = y 2

Como y = a 1 - x L + x 2 L 2 , temos que:

y - e l = a 2 1 - x L + x 2 L 2

Analisando a área do elemento, temos que:

d A = y d x

d A = a 1 - x L + x 2 L 2 d x

Passo 2

Para encontrar a área usando a integração direta, temos que:

A = ∫ d A

Portanto:

∫ d A = ∫ 0 2 L a 1 - x L + x 2 L 2 d x

Resolvendo a integral, temos que:

A = a x - x 2 2 L + x 3 3 L 2 0 2 L

A = a 2 L - 2 L 2 2 L + 2 L 3 3 L 2 - 0 + 0 - 0

A = 8 a L 3

Passo 3

Agora que descobrimos A , podemos aplicar que:

x - A = ∫ x - e l d A

E:

y - A = ∫ y - e l d A

Vamos encontrar as integrais para assim descobrir o centroide do sistema.

Passo 4

Temos que:

∫ x - e l d A = ∫ 0 2 L x a 1 - x L + x 2 L 2 d x

Resolvendo, temos que:

∫ x - e l d A = a x 2 2 - x 3 3 L + x 4 4 L 2 0 2 L

∫ x - e l d A = a 2 L 2 2 - 2 L 3 3 L + 2 L 4 4 L 2 - 0 + 0 - 0

∫ x - e l d A = a 2 L 2 - 8 L 2 3 + 4 L 2

Portanto:

∫ x - e l d A = 10 a L 2 3

Passo 5

Temos também que:

∫ y - e l d A = ∫ 0 2 L a 2 1 - x L + x 2 L 2 a 1 - x L + x 2 L 2 d x

∫ y - e l d A = a 2 2 ∫ 0 2 L 1 - x L + x 2 L 2 2 d x

∫ y - e l d A = a 2 2 ∫ 0 2 L 1 + x 2 L 2 + x 4 L 4 - 2 x L + 2 x 2 L 2 - 2 x 3 L 3 d x

Resolvendo, temos que:

∫ y - e l d A = a 2 2 x + x 3 3 L 2 + x 5 5 L 4 - 2 x 2 2 L + 2 x 3 3 L 2 - 2 x 4 4 L 3 0 2 L

∫ y - e l d A = a 2 2 2 L + 2 L 3 3 L 2 + 2 L 5 5 L 4 - 2 2 L 2 2 L + 2 2 L 3 3 L 2 - 2 2 L 4 4 L 3

∫ y - e l d A = a 2 2 2 L + 8 L 3 + 32 L 5 - 4 L + 16 L 3 - 8 L

Portanto:

∫ y - e l d A = 11 a 2 L 5

Passo 6

Agora é só aplicar. Temos que:

x - A = ∫ x - e l d A

x - 8 a L 3 = 10 a L 2 3

x - = 10 a L 2 3 ⋅ 3 8 a L

Portanto:

x - = 5 L 4

Aplicando:

y - A = ∫ y - e l d A

Temos que:

y - 8 a L 3 = 11 a 2 L 5

y - = 11 a 2 L 5 ⋅ 3 8 a L

Portanto:

y - = 33 a 40

Sendo assim o centroide representado por:

x - ,   y - = 5 L 4 , 33 a 40

Resposta

x - ,   y - = 5 L 4 , 33 a 40

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume do material necessário para realizar a moldagem.
O trocador de calor irradia energia térmica a uma taxa de 2500k J / h para cada metro quadrado de sua área superficial. Determine quantos joules ( J ) são irradiados dentro de um período de 5 horas.
Determine a altura h à qual o líquido deve ser vertido dentro do copo cônico de modo que atinja três quartos da área de superfície no interior do copo. Para o cálculo, desconsidere a espessura do copo
A corrente da esquerda para a direita no fluxo causa um arrasto uniforme de 4 lb por pé do fluxo cruzado no cabo flutuante que é conectado aos postes A e B. Determine as tensões mínimas e máximas no c
Um rebocador motorizado reboca uma barcaça com um cabo que tem uma massa de 14 kg por metro de comprimento. Observa-se que a tangente ao cabo no ponto A é horizontal. Determine as tensões em A e B.