50. Usando uma peça anelar, a força de pode ser aplicada no plano vertical para vários ângulos . Determine a intensidade do momento produzido em relação ao ponto . Faça um gráfico do resultado de (na ordenada) versus (na abscissa) para e especifique os ângulos que fornecem os momentos máximo e mínimo.
Passo 1
Para fornecer o resultado como o enunciado pede precisamos calcular o momento da força usando o produto vetorial que é dado da seguinte maneira:
Onde:
representam as coordenadas do vetor posição definido a partir do ponto que queremos calcular o momento até qualquer ponto na linha de aplicação da força.
são as componentes da força aplicada.
Para saber as coordenadas do vetor , basta olhar a figura e ver quanto você tem que andar para cada direção para chegar ao ponto na linha de ação da força, logo:
Tendo encontrado o momento, teremos ele na forma vetorial, então teremos que calcular a norma desse vetor para obtermos a intensidade do momento.
Tendo esses resultados ainda falta saber os pontos máximos e mínimos para marcarmos no gráfico. para achar esse ângulo podemos usar uma propriedade da derivada ao nosso favor, que é o derivarmos essa função com respeito a e igualar a , encontrando o que faz isso e teremos assim os máximos e os mínimos da função.
Passo 2
Agora que já temos tudo que precisamos, vamos calcular o momento em relação ao ponto .
Passo 3
Nós encontramos o momento na forma vetorial, agora vamos calcular a intensidade dele através da norma dele.
Passo 4
Antes de partimos para o gráfico temos que encontrar os pontos críticos dessa pequena função (kkkk), e faremos isso usando a derivada ao nosso fazer, calculando a derivada da função, igualando a e vendo quais , tornam a igualdade verdadeira.
Dentro do limite estabelecido pelo enunciado , temos:
Para esses valores de , temos:
E temos para com ou :
Passo 5
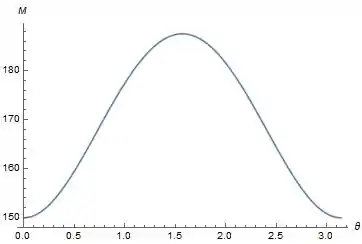
Agora abaixo temos o gráfico como é pedido no enunciado.