Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 162
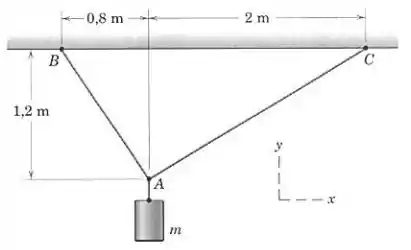
Usando os princípios de equilíbrio que serão desenvolvidos no Capítulo , brevemente você será capaz de verificar que a força trativa no cabo vale do peso do cilindro de massa , enquanto a força trativa no cabo vale do peso suspenso. Escreva cada força trativa atuando no ponto como um vetor, se a massa vale .
Passo 1
De acordo com as dimensões da figura, o ângulo que o cabo faz com a horizontal é:
E o ângulo que o cabo faz com a horizontal é:
Passo 2
Sendo assim, podemos escrever o vetor :
E também o vetor :
Resposta
Exercícios de Livros Relacionados
Expresse F1 e F2 como vetores cartesianos.
Determine a intensidade da força resultante e sua direção, medida em sentido anti-horário a partir do eixo positivo x .
Determine a intensidade e a orientação, medida no sentido anti-horário a partir do eixo y positivo, da força resultante que atua no suporte, se FB = 600 N e θ=20 ° .
Se F1 = 300 N e θ=10 ° , determine a intensidade da força resultante que atua sobre o suporte e sua direção, medida no sentido anti-horário a partir do eixo positivo x’.
Três forças atuam sobre o suporte. Determine a intensidade e a direção de F1, de modo que a força resultante seja direcionada ao longo do eixo x’ positivo e tenha uma intensidade de 800 N.