Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.9 - Ex. 159
A resultante das duas forças e do torque pode ser representada por um torçor. Determine a expressão vetorial para o momento do torçor e encontre as coordenadas do ponto no plano pelo qual passa a força resultante do torçor.
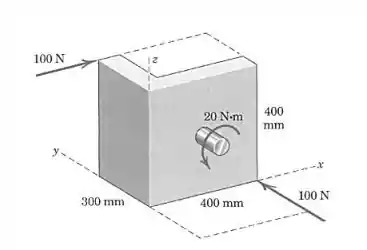
Passo 1
Queremos que a força resultante R seja representada como sendo aplicada num ponto , e que o momento resultante M das forças e do torque no ponto seja paralelo a essa força resultante. Então devemos calcular R e M no ponto e após isso igualar os dois vetores diretores unitários.
Passo 2
Primeiro, calculamos a força resultante:
Agora, achamos o vetor unitário de R, sendo R o módulo de R:
Passo 3
Agora devemos calcular o momento resultante das duas forças e do torque no ponto . A força paralela ao eixo causa um momento em torno do eixo , com uma distância de 0,3 m e no sentido negativo (dado pela regra da mão direita) e outro momento em torno do eixo , com uma distância de m e no sentido positivo.
A força paralela ao eixo causa um momento em torno do eixo com uma distância de m no sentido positivo e um momento em torno do eixo com uma distância m no sentido positivo.
Agora somamos os dois momentos com o torque de N.m:
Passo 4
Agora devemos garantir que o vetor unitário de M seja . Temos:
Isso nos dá 3 equações:
Dessas duas tiramos o valor de :
Da terceira equação achamos
Agora substituímos e para achar o valor de M: