Na posição mostrada, o virabrequim de um pequeno compressor de dois cilindros está submetido a forças de 400 N e 800 N, exercidas pelas bielas, e um torque de 200 N.m. Substitua esse sistema de carregamento por um sistema força-binário no ponto A. Mostre que não é perpendicular a . Substitua, então, esse sistema força-binário por um torçor. Determine o módulo do momento do torçor, o módulo da força do torçor, e as coordenadas do ponto no plano pelo qual passa a linha de ação do torçor.
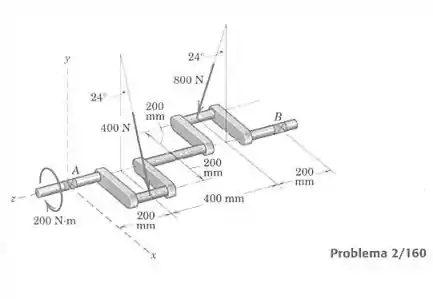
Passo 1
Queremos inicialmente calcular a força resultante e o momento resultante no ponto A. A força de 400 N pode ser decomposta assim:
Decompomos agora a força de 800 N:
A força resultante será então:
Passo 2
Agora devemos calcular o momento resultante causado pelas forças e o torque. O torque é igual a . Calculamos agora o momento causado pela força de 400 N:
Agora o momento causado pela força de 800 N:
Então o momento total no ponto A será:
Passo 3
Agora devemos verificar se é perpendicular a . Quando dois vetores são perpendiculares sabemos que o produto interno entre eles dá zero. Efetuando então o produto:
Logo, a força resultante não é perpendicular ao momento resultante.
Passo 4
Queremos agora substituir a força por um torçor, passando por um ponto . Um torçor é composto por uma força R e um momento M paralelo à força. Já calculamos a força R, temos agora que encontrar M em relação ao ponto e então garantir que seja paralelo a R. Vamos achar o vetor unitário de R:
Passo 5
Precisamos agora achar o momento em relação ao ponto . Primeiro o momento da força de 400 N:
Agora da força de 800 N:
O momento do torçor será então:
Passo 6
O momento do torçor deve ser paralelo ao da força resultante, então os vetores unitários que representam a direção dos dois vetores devem ser iguais. Temos:
Mas já calculamos que:
Então:
Isso nos dá então 3 quações:
Através de descobrimos o módulo de :