Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 77

Usando o teorema dos eixos paralelos, determine o produto de inércia da figura:

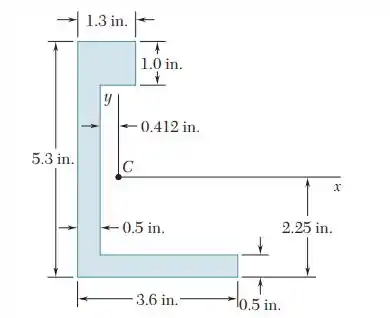
Passo 1

Fala aí galera, vamos pra mais um problema de estática. Sabemos que o teorema dos eixos paralelos diz que:

I x y = I x ' y ' + x - y - A

Podemos perceber que os 3 retângulos possuem eixo de simetria e portanto possuem seu produto de inércia nulo, logo, pelo teorema dos eixos paralelos:

I x y 1 = 0 + 1,8 - 0,912 0,25 - 2,25 0,5 × 3,6 = - 3,1968

I x y 2 = 0 + 0,25 - 0,912 2,65 - 2,25 0,5 × 5,3 = - 0,70172

I x y 3 = 0 + 0,65 - 0,912 4,8 - 2,25 1,3 × 1 = - 0,86853

Logo:

I x y = - 3,1968 - 0,70172 - 0,86853 = - 4,76705

Portanto:

I x y = I x ' y ' + x - y - A

- 4,76705 - 0,912 × 2,25 × 5,75 = I x ' y '

I x ' y ' = - 16,566   i n 4  

Resposta

I x ' y ' = - 16,566   i n 4

Ver Outros Exercícios desse livro