Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 76

Usando o teorema dos eixos paralelos, determine o produto de inércia da superfície mostrada na figura em relação aos eixos centroidais x e y .

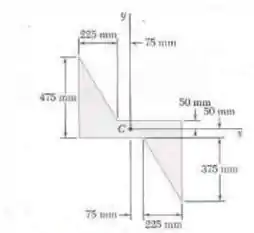
Passo 1

Fala aí galera, vamos para mais um problema de estática. Sabemos que o teorema dos eixos paralelos diz que:

I x y = I x ' y ' + x - y - A

Podemos perceber que o eixo de simetria do retângulo implica que seu produto de inércia seja nulo, assim como I x ' y ' . Logo, pelo teorema dos eixos paralelos:

I x y 1 = 0 + - 2 3 × 225 + 75 1 3 × 375 + 75 375 × 225 2     = - 632812500   m m 4

I x y 2 = 0 + 2 3 × 225 + 75 - 1 3 × 37 5 + 75 375 × 225 2 = - 632812500   m m 4

Logo:

I x y = - 632812500 - 632812500

I x y = 1265625000   m m 4

Resposta

I x y = 1265625000   m m 4

Ver Outros Exercícios desse livro